Bewise Inc. www.tool-tool.com Reference source from the internet.
In der Geometrie ist ein Normalenvektor ein Vektor, der senkrecht (orthogonal) auf einer Geraden, Kurve, Ebene, (gekrümmten) Fläche oder einer höherdimensionalen Verallgemeinerung eines solchen Objekts steht. Die Gerade, die diesen Vektor als Richtungsvektor besitzt, heißt Normale. Ein Normaleneinheitsvektor ist ein Normalenvektor der Länge 1 (ein sogenannter normierter Vektor).
In diesem Artikel wird zunächst der Fall der Geraden (in einer Ebene) und der Ebene (im dreidimensionalen Raum) behandelt (Lineare Algebra und analytische Geometrie), dann der Fall der ebenen Kurve und der Fläche (Differentialgeometrie).
Lineare Algebra und analytische Geometrie [Bearbeiten]
In diesem Abschnitt werden die Variablen für Vektoren, wie in der Schulmathematik üblich, durch Vektorpfeile gekennzeichnet.
Normale und Normalenvektor einer Geraden [Bearbeiten]
Ein Normalenvektor einer Geraden g in der Ebene ist ein (vom Nullvektor verschiedener) Vektor, der senkrecht auf dieser Geraden steht, also der Richtungsvektor einer Geraden, die senkrecht auf g steht (Orthogonale oder Normale zu g).
Hat g den Richtungsvektor  , so sind die beiden Vektoren ( − b,a) und (b, − a) Normalenvektoren. Durchläuft man die Gerade in der Richtung von
, so sind die beiden Vektoren ( − b,a) und (b, − a) Normalenvektoren. Durchläuft man die Gerade in der Richtung von  , so weist ( − b,a) nach links und (b, − a) nach rechts.
, so weist ( − b,a) nach links und (b, − a) nach rechts.
Ist die Gerade in der Steigungsform durch die Gleichung
- y = mx + c
gegeben, so ist der Vektor (1,m) ein Richtungsvektor der Geraden und ( − m,1) und (m, − 1) sind Normalenvektoren. Für  hat also jede Normale die Steigung
hat also jede Normale die Steigung  . Ist m = 0, also g horizontal, so ist jede Normale vertikal, hat also eine Gleichung der Form x = a.
. Ist m = 0, also g horizontal, so ist jede Normale vertikal, hat also eine Gleichung der Form x = a.
Ist die Gerade in der allgemeinen Form
- ax + by = d
gegeben, so ist (a,b) ein Normalenvektor.
Hat man einen Normalenvektor, so erhält man einen Normaleneinheitsvektor, indem man diesen durch seine Länge (Norm, Betrag) dividiert (den Vektor also normiert). Einen zweiten Normalenvektor erhält man durch Multiplikation mit − 1. Aus einem Normalenvektor erhält man alle anderen durch Multiplikation mit einer reellen Zahl ungleich null.
Normale und Normalenvektor einer Ebene [Bearbeiten]
Ein Normalenvektor einer Ebene E im dreidimensionalen Raum ist ein (vom Nullvektor verschiedener) Vektor, der senkrecht auf dieser Ebene steht, also der Richtungsvektor einer Geraden, die senkrecht auf E steht (Orthogonale oder Normale zu g).
Ist die Ebene in der Normalform
- ax + by + cz = d
gegeben, so ist (a,b,c) ein Normalenvektor.
Ist E durch zwei aufspannende Vektoren 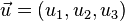 und
und  gegeben (Punkt-Richtungs-Form oder Parameterform), führt die Bedingung, dass der Normalenvektor
gegeben (Punkt-Richtungs-Form oder Parameterform), führt die Bedingung, dass der Normalenvektor  senkrecht auf
senkrecht auf  und
und 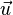 steht, ein lineares Gleichungssystem für die Komponenten n1,n2,n3 von
steht, ein lineares Gleichungssystem für die Komponenten n1,n2,n3 von  :
:
Jede von (0,0,0) verschiedene Lösung liefert einen Normalenvektor.
Eine andere Möglichkeit, Normalenvektoren zu bestimmen, bietet das Kreuzprodukt:
ist ein Vektor, der senkrecht auf  und
und  steht, und
steht, und  bilden in dieser Reihenfolge ein Rechtssystem.
bilden in dieser Reihenfolge ein Rechtssystem.
Hat E die Gleichung
- z = ax + by + c,
so ist ( − a, − b,1) ein nach oben weisender und (a,b, − 1) ein nach unten weisender Normalenvektor.
Wie im Fall der Geraden in der Ebene erhält man aus einem Normalenvektor einen Normaleneinheitsvektor, indem man ihn durch seine Länge dividiert, einen zweiten durch Multiplikation mit − 1 und alle andern Normalenvektor durch Multiplikation mit reellen Zahlen.
Eine Ebene wird durch einen Normalenvektor sowie einen auf der Ebene liegenden Punkt eindeutig bestimmt, siehe Normalenform und Hessesche Normalform.
Normalenvektoren von Kurven und Flächen [Bearbeiten]
ebene Kurven [Bearbeiten]
In der Analysis und in der Differentialgeometrie ist der Normalenvektor zu einer ebenen Kurve (in einem bestimmten Punkt) ein Vektor, der auf der Tangente in diesem Punkt orthogonal (senkrecht) steht. Die Gerade in Richtung des Normalenvektors durch diesen Punkt heißt Normale.
Ist die Kurve als Graph einer differenzierbaren Funktion f gegeben, so hat die Tangente im Punkt p = (x0,f(x0)) die Steigung  , die Steigung der Normalen beträgt also
, die Steigung der Normalen beträgt also
Die Normale im Punkt p = (x0,f(x0)) ist dann durch die Gleichung
- y = f(x0) + mn(x − x0),
also durch
gegeben.
Ist die ebene Kurve in Parameterform gegeben, c(t) = (c1(t),c2(t)), so ist 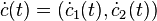 ein Tangentialvektor im Punkt c(t) und
ein Tangentialvektor im Punkt c(t) und 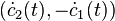 ein nach rechts weisender Normalenvektor. Hier bezeichnet, wie in der Differentialgeometrie üblich, der Punkt die Ableitung nach dem Kurvenparameter.
ein nach rechts weisender Normalenvektor. Hier bezeichnet, wie in der Differentialgeometrie üblich, der Punkt die Ableitung nach dem Kurvenparameter.
Bei Raumkurven bilden die Normalenvektoren in einem Punkt (wie im Fall der Geraden im Raum) einen zweidimensionalen Untervektorraum. In der elementaren Differentialgeometrie wählt man einen Einheitsvektor aus, der in die Richtung zeigt, in die die Kurve gekrümmt ist. Diesen nennt man Hauptnormalen(einheits)vektor, siehe Frenetsche Formeln.
Flächen im dreidimensionalen Raum [Bearbeiten]
Entsprechend ist der Normalenvektor einer gekrümmten Fläche (Topologie) in einem Punkt der Normalenvektor der Tangentialebene in diesem Punkt.
Ist die Fläche durch die Parameterdarstellung
gegeben, so spannen die beiden Vektoren
 und
und 
die Tangentialebene im Punkt F(u,v) auf. (Hier wird vorausgesetzt, dass die Fläche bei (u,v) regulär ist, also dass Fu(u,v) und Fu(u,v) linear unabhängig sind.) Ein Normalenvektor im Punkt F(u,v) ist ein Vektor, der senkrecht auf Fu(u,v) und Fu(u,v) steht, z. B. der durch das Kreuzprodukt gegebene und dann normierte Hauptnormalenvektor
Hier bezeichnen die Betragsstriche die euklidische Norm des Vektors.
Ist die Fläche implizit durch eine Gleichung gegeben,
- g(x,y,z) = 0,
wobei  eine differenzierbare Funktion ist, so ist der Gradient
eine differenzierbare Funktion ist, so ist der Gradient
ein Normalenvektor der Fläche im Punkt (x,y,z) (vorausgesetzt, dass er dort nicht verschwindet).
Ist die Fläche als Graph einer differenzierbaren Funktion 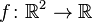 gegeben, so ist
gegeben, so ist
ein nach oben weisender Normalenvektor im Punkt p = (x,y,f(x,y)). Dies erhält man, indem man verwendet, dass die Abbildung F(x,y) = (x,y,F(x,y)) eine Parametrisierung ist oder dass die Fläche durch die Gleichung
- g(x,y,z): = z − f(x,y) = 0
dargestellt wird.
Verallgemeinerungen [Bearbeiten]
Der Begriff des Normalenvektors lässt sich verallgemeinern auf
- affine Unterräume (verallgemeinerte Ebenen) in euklidischen Räumen höherer Dimension (Mathematik) (insbesondere auf Hyperebenen),
- Flächen, Hyperflächen und Untermannigfaltigkeiten in euklidischen Räumen höherer Dimension,
- Flächen, Hyperflächen und Untermannigfaltigkeiten von Riemannsichen Mannigfaltigkeiten,
- Nichtglatte Objekte, wie konvexe Körper und rektifizierbare Mengen.
Anwendungen [Bearbeiten]
Im Bereich der Computergrafik werden Normalenvektoren genutzt, um festzustellen, ob eine Fläche dem Benutzer zugewandt ist oder nicht. Der Einsatz von Normalenvektoren erlaubt dadurch Back Face Culling.
歡迎來到Bewise Inc.的世界,首先恭喜您來到這接受新的資訊讓產業更有競爭力,我們是提供專業刀具製造商,應對客戶高品質的刀具需求,我們可以協助客戶滿足您對產業的不同要求,我們有能力達到非常卓越的客戶需求品質,這是現有相關技術無法比擬的,我們成功的滿足了各行各業的要求,包括:精密HSS DIN切削刀具、協助客戶設計刀具流程、DIN or JIS 鎢鋼切削刀具設計、NAS986 NAS965 NAS897 NAS937orNAS907 航太切削刀具,NAS航太刀具設計、超高硬度的切削刀具、醫療配件刀具設計、汽車業刀具設計、電子產業鑽石刀具、木工產業鑽石刀具等等。我們的產品涵蓋了從民生刀具到工業級的刀具設計;從微細刀具到大型刀具;從小型生產到大型量產;全自動整合;我們的技術可提供您連續生產的效能,我們整體的服務及卓越的技術,恭迎您親自體驗!!
BW Bewise Inc. Willy Chen willy@tool-tool.com bw@tool-tool.com www.tool-tool.com skype:willy_chen_bw mobile:0937-618-190 Head &Administration Office No.13,Shiang Shang 2nd St., West Chiu Taichung,Taiwan 40356 http://www.tool-tool..com / FAX:+886 4 2471 4839 N.Branch 5F,No.460,Fu Shin North Rd.,Taipei,Taiwan S.Branch No.24,Sec.1,Chia Pu East Rd.,Taipao City,Chiayi Hsien,Taiwan
Welcome to BW tool world! We are an experienced tool maker specialized in cutting tools. We focus on what you need and endeavor to research the best cutter to satisfy users’ demand. Our customers involve wide range of industries, like mold & die, aerospace, electronic, machinery, etc. We are professional expert in cutting field. We would like to solve every problem from you. Please feel free to contact us, its our pleasure to serve for you. BW product including: cutting tool、aerospace tool .HSS DIN Cutting tool、Carbide end mills、Carbide cutting tool、NAS Cutting tool、NAS986 NAS965 NAS897 NAS937orNAS907 Cutting Tools,Carbide end mill、disc milling cutter,Aerospace cutting tool、hss drill’Фрезеры’Carbide drill、High speed steel、Milling cutter、CVDD(Chemical Vapor Deposition Diamond )’PCBN (Polycrystalline Cubic Boron Nitride) ’Core drill、Tapered end mills、CVD Diamond Tools Inserts’PCD Edge-Beveling Cutter(Golden Finger’PCD V-Cutter’PCD Wood tools’PCD Cutting tools’PCD Circular Saw Blade’PVDD End Mills’diamond tool ‘Single Crystal Diamond ‘Metric end mills、Miniature end mills、Специальные режущие инструменты ‘Пустотелое сверло ‘Pilot reamer、Fraises’Fresas con mango’ PCD (Polycrystalline diamond) ‘Frese’Electronics cutter、Step drill、Metal cutting saw、Double margin drill、Gun barrel、Angle milling cutter、Carbide burrs、Carbide tipped cutter、Chamfering tool、IC card engraving cutter、Side cutter、NAS tool、DIN or JIS tool、Special tool、Metal slitting saws、Shell end mills、Side and face milling cutters、Side chip clearance saws、Long end mills、Stub roughing end mills、Dovetail milling cutters、Carbide slot drills、Carbide torus cutters、Angel carbide end mills、Carbide torus cutters、Carbide ball-nosed slot drills、Mould cutter、Tool manufacturer.
ようこそBewise Inc.の世界へお越し下さいませ、先ず御目出度たいのは新たな
情報を受け取って頂き、もっと各産業に競争力プラス展開。
弊社は専門なエンド・ミルの製造メーカーで、客先に色んな分野のニーズ、
豊富なパリエーションを満足させ、特にハイテク品質要求にサポート致します。
弊社は各領域に供給できる内容は:
(3)鎢鋼エンド・ミル設計
(4)航空エンド・ミル設計
(5)超高硬度エンド・ミル
(7)医療用品エンド・ミル設計
弊社の製品の供給調達機能は:
(4)オートメーション整備調達
弊社の全般供給体制及び技術自慢の総合専門製造メーカーに貴方のご体験を御待ちしております。
BW специализируется в научных исследованиях и разработках, и снабжаем самым высокотехнологичным карбидовым материалом для поставки режущих / фрезеровочных инструментов для почвы, воздушного пространства и электронной индустрии. В нашу основную продукцию входит твердый карбид / быстрорежущая сталь, а также двигатели, микроэлектрические дрели, IC картонорезальные машины, фрезы для гравирования, режущие пилы, фрезеры-расширители, фрезеры-расширители с резцом, дрели, резаки форм для шлицевого вала / звездочки роликовой цепи, и специальные нано инструменты. Пожалуйста, посетите сайт www.tool-tool.com для получения большей информации.
BW is specialized in R&D and sourcing the most advanced carbide material with high-tech coating to supply cutting / milling tool for mould & die, aero space and electronic industry. Our main products include solid carbide / HSS end mills, micro electronic drill, IC card cutter, engraving cutter, shell end mills, cutting saw, reamer, thread reamer, leading drill, involute gear cutter for spur wheel, rack and worm milling cutter, thread milling cutter, form cutters for spline shaft/roller chain sprocket, and special tool, with nano grade. Please visit our web www.tool-tool.com for more info.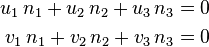
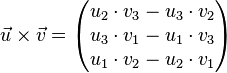
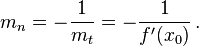



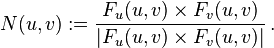


No comments:
Post a Comment