Bewise Inc. www.tool-tool.com Reference source from the internet.
The cut-elimination theorem is the central result establishing the significance of the sequent calculus. It was originally proved by Gerhard Gentzen 1934 in his landmark paper "Investigations in Logical Deduction" for the systems LJ and LK formalising intuitionistic and classical logic respectively. The cut-elimination theorem (Hauptsatz) states that any judgement that possesses a proof in the sequent calculus that makes use of the cut rule also possesses a cut-free proof, that is, a proof that does not make use of the cut rule.
A sequent is a logical expression relating multiple sentences, in the form "
", which is to be read as "A, B, C,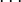 
proves N, O, P", and (as glossed by Gentzen) should be understood as equivalent to the truth-function "If (A and B and C 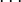) then (N or O or P)." Note that the left-hand side (LHS) is a conjunction (and) and the RHS is a disjunction (or). The LHS may have arbitrarily many or few formulae; when the LHS is empty, the RHS is a tautology. In LK, the RHS may also have any number of formulae—if it has none, the LHS is a contradiction, whereas in LJ the RHS may have only none or one formula: here we see that allowing more than one formula in the RHS is equivalent, in the presence of the right contraction rule, to the admissibility of the law of the excluded middle. However, the sequent calculus is a fairly expressive framework, and there have been sequent calculi for intuitionistic logic proposed that allow many formulae in the RHS. From Jean-Yves Girard's logic LC it is easy to obtain a rather natural formalisation of classical logic where the RHS contains at most one formula; it is the interplay of the logical and structural rules that is the key here.
"Cut" is a rule in the normal statement of the sequent calculus, and equivalent to a variety of rules in other proof theories, which, given
- (1)
and
- (2)
allows one to infer
- (3)
That is, it "cuts" the occurrences of the formula "C" out of the inferential relation.
The cut-elimination theorem states that (for a given system) any sequent provable using the rule Cut can be proved without use of this rule. If we think of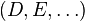 
as a theorem, then cut-elimination simply says that a lemma C used to prove this theorem can be inlined. Whenever the theorem's proof mentions lemma C, we can substitute the occurrences for the proof of C. Consequently, the cut rule is admissible.
For systems formulated in the sequent calculus, analytic proofs are those proofs that do not use Cut. Typically such a proof will be longer, of course, and not necessarily trivially so. In his essay "Don't Eliminate Cut!" George Boolos demonstrated that there was a derivation that could be completed in a page using cut, but whose analytic proof could not be completed in the lifespan of the universe.
The theorem has many, rich consequences:
- A system is inconsistent if it admits a proof of the absurd. If the system has a cut elimination theorem, then if it has a proof of the absurd, it should also have a proof of the absurd without cuts. It is typically very easy to check that there are no such proofs. Thus, once a system is shown to have a cut elimination theorem, it is normally immediate that the system is consistent.
- Normally also the system has the subformula property, an important property in several approaches to proof-theoretic semantics.
Cut elimination is one of the most powerful tools for proving interpolation theorems. The possibility of carrying out proof search based on resolution, the essential insight leading to the Prolog programming language, depends upon the admissibility of Cut in the appropriate system.
For proof systems based on higher-order lambda calculus through a Curry-Howard isomorphism, cut elimination algorithms correspond to the strong reduction property (every proof term has a normal form and this normal form is reached by any complete sequence of reductions).
[edit] See also
[edit] References
Gentzen, Gerhard (1934-1935). "Untersuchungen über das logische Schließen". Mathematische Zeitschrift 39: 405-431.歡迎來到Bewise Inc.的世界，首先恭喜您來到這接受新的資訊讓產業更有競爭力，我們是提供專業刀具製造商，應對客戶高品質的刀具需求，我們可以協助客戶滿足您對產業的不同要求，我們有能力達到非常卓越的客戶需求品質，這是現有相關技術無法比擬的，我們成功的滿足了各行各業的要求，包括：精密HSS DIN切削刀具、協助客戶設計刀具流程、DIN or JIS 鎢鋼切削刀具設計、NAS986 NAS965 NAS897 NAS937orNAS907 航太切削刀具,NAS航太刀具設計、超高硬度的切削刀具、醫療配件刀具設計、汽車業刀具設計、電子產業鑽石刀具、木工產業鑽石刀具等等。我們的產品涵蓋了從民生刀具到工業級的刀具設計；從微細刀具到大型刀具；從小型生產到大型量產；全自動整合；我們的技術可提供您連續生產的效能，我們整體的服務及卓越的技術，恭迎您親自體驗！！
BW Bewise Inc. Willy Chen willy@tool-tool.com bw@tool-tool.com www.tool-tool.com skype:willy_chen_bw mobile:0937-618-190 Head &Administration Office No.13,Shiang Shang 2nd St., West Chiu Taichung,Taiwan 40356 http://www.tool-tool..com / FAX:+886 4 2471 4839 N.Branch 5F,No.460,Fu Shin North Rd.,Taipei,Taiwan S.Branch No.24,Sec.1,Chia Pu East Rd.,Taipao City,Chiayi Hsien,Taiwan
Welcome to BW tool world! We are an experienced tool maker specialized in cutting tools. We focus on what you need and endeavor to research the best cutter to satisfy users’ demand. Our customers involve wide range of industries, like mold & die, aerospace, electronic, machinery, etc. We are professional expert in cutting field. We would like to solve every problem from you. Please feel free to contact us, its our pleasure to serve for you. BW product including: cutting tool、aerospace tool .HSS DIN Cutting tool、Carbide end mills、Carbide cutting tool、NAS Cutting tool、NAS986 NAS965 NAS897 NAS937orNAS907 Cutting Tools,Carbide end mill、disc milling cutter,Aerospace cutting tool、hss drill’Фрезеры’Carbide drill、High speed steel、Milling cutter、CVDD(Chemical Vapor Deposition Diamond )’PCBN (Polycrystalline Cubic Boron Nitride) ’Core drill、Tapered end mills、CVD Diamond Tools Inserts’PCD Edge-Beveling Cutter(Golden Finger’PCD V-Cutter’PCD Wood tools’PCD Cutting tools’PCD Circular Saw Blade’PVDD End Mills’diamond tool ‘Single Crystal Diamond ‘Metric end mills、Miniature end mills、Специальные режущие инструменты ‘Пустотелое сверло ‘Pilot reamer、Fraises’Fresas con mango’ PCD (Polycrystalline diamond) ‘Frese’Electronics cutter、Step drill、Metal cutting saw、Double margin drill、Gun barrel、Angle milling cutter、Carbide burrs、Carbide tipped cutter、Chamfering tool、IC card engraving cutter、Side cutter、NAS tool、DIN or JIS tool、Special tool、Metal slitting saws、Shell end mills、Side and face milling cutters、Side chip clearance saws、Long end mills、Stub roughing end mills、Dovetail milling cutters、Carbide slot drills、Carbide torus cutters、Angel carbide end mills、Carbide torus cutters、Carbide ball-nosed slot drills、Mould cutter、Tool manufacturer.
ようこそＢｅｗｉｓｅ Ｉｎｃ.の世界へお越し下さいませ、先ず御目出度たいのは新たな
情報を受け取って頂き、もっと各産業に競争力プラス展開。
弊社は専門なエンド・ミルの製造メーカーで、客先に色んな分野のニーズ、
豊富なパリエーションを満足させ、特にハイテク品質要求にサポート致します。
弊社は各領域に供給できる内容は：
（３）鎢鋼エンド・ミル設計
（４）航空エンド・ミル設計
（５）超高硬度エンド・ミル
（７）医療用品エンド・ミル設計
弊社の製品の供給調達機能は：
（４）オートメーション整備調達
弊社の全般供給体制及び技術自慢の総合専門製造メーカーに貴方のご体験を御待ちしております。
BW специализируется в научных исследованиях и разработках, и снабжаем самым высокотехнологичным карбидовым материалом для поставки режущих / фрезеровочных инструментов для почвы, воздушного пространства и электронной индустрии. В нашу основную продукцию входит твердый карбид / быстрорежущая сталь, а также двигатели, микроэлектрические дрели, IC картонорезальные машины, фрезы для гравирования, режущие пилы, фрезеры-расширители, фрезеры-расширители с резцом, дрели, резаки форм для шлицевого вала / звездочки роликовой цепи, и специальные нано инструменты. Пожалуйста, посетите сайт www.tool-tool.com для получения большей информации.
BW is specialized in R&D and sourcing the most advanced carbide material with high-tech coating to supply cutting / milling tool for mould & die, aero space and electronic industry. Our main products include solid carbide / HSS end mills, micro electronic drill, IC card cutter, engraving cutter, shell end mills, cutting saw, reamer, thread reamer, leading drill, involute gear cutter for spur wheel, rack and worm milling cutter, thread milling cutter, form cutters for spline shaft/roller chain sprocket, and special tool, with nano grade. Please visit our web www.tool-tool.com for more info.
No comments:
Post a Comment