Bewise Inc. www.tool-tool.com Reference source from the internet.
Una corrente elettrica i che scorre in un circuito elettrico produce un campo magnetico nello spazio circostante e un flusso magnetico Φ attraverso il circuito. Le linee del campo di induzione magnetica si concatenano col circuito che le ha generate e pertanto se la corrente varia nel tempo, risulta variabile il flusso magnetico concatenato determinando entro il circuito una f.e.m. indotta. L'induttanza o coefficiente di autoinduzione del circuito è quindi il rapporto tra il flusso magnetico generato e la corrente passante. Va osservato anche che, se il mezzo che circonda il circuito elettrico è a permeabilità costante (mezzo lineare), il flusso concatenato con esso risulta proporzionale alla corrente che scorre nel circuito; infatti l'induzione magnetica generata in ogni istante da un circuito è per l'appunto proporzionale all'intensità che la corrente ivi circolante ha in quel preciso istante e quindi:  dove L è appunto la costante di proporzionalità menzionata
dove L è appunto la costante di proporzionalità menzionata
Il termine fu utilizzato per la prima volta da Oliver Heaviside nel Febbraio 1886.[1] L'induttanza si indica con la lettera L maiuscola.
La definizione operativa di induttanza di una spira di corrente è data dalla seguente relazione:
In onore di Joseph Henry, all'unità di misura dell'induttanza è stato dato il nome henry (H) : 1 H = 1 Wb /1 A.
L'induttanza è anche detta coefficiente di autoinduzione del circuito.
Indice
[nascondi]- 1 Proprietà dell'induttanza
- 2 Cenni sull'induttore
- 3 Circuito RL
- 4 Circuito RLC
- 5 Note
- 6 Bibliografia
- 7 Voci correlate
Proprietà dell'induttanza [modifica]
L'equazione che definisce l'induttanza può essere girata in questo modo:
Derivando entrambi i membri rispetto al tempo:
In molti casi fisici l'induttanza può essere considerata costante (o tempo-invariante), per cui:
Dalla legge di Faraday si ha:
dove 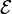 è la forza elettromotrice (f.e.m.) e v è il potenziale indotto ai morsetti del circuito in questione.
è la forza elettromotrice (f.e.m.) e v è il potenziale indotto ai morsetti del circuito in questione.
Combinando le equazioni precedenti si ha:
da cui si evince che l'induttanza L di un componente attraversato da corrente variabile si può definire operativamente come l'opposto del rapporto tra la f.e.m autoindotta ε generata ai morsetti del componente e la derivata della corrente di(t)/dt che lo attraversa.
L'origine del segno meno è una conseguenza della legge di Lenz che applicata a un induttore afferma in sostanza che la f.e.m autoindotta ai capi di un componente si oppone alla variazione di corrente che lo attraversa. Per questo motivo l'induttanza è definita positiva.
L'energia immagazzinata in un solenoide può essere espressa per mezzo della sua induttanza caratteristica L e della corrente i che scorre nelle sue spire.
La relazione è

dove W è l'energia immagazzinata.
La legge di Ohm esprime la relazione fra la tensione e una corrente stazionaria, mentre quella di Faraday il legame fra tensione e una corrente elettrica variabile.
Cenni sull'induttore [modifica]
![]()
Per approfondire, vedi la voce Induttore.
In termini circuitali, l'induttore è un componente passivo in cui l'aspetto induttivo prevale su quello capacitivo e su quello resistivo. Esso è generalmente costituito dall'avvolgimento di un filo conduttore intorno ad un nucleo di materiale magnetico (ferrite). La relazione costitutiva di un induttore di induttanza L è la stessa riportata sopra. Valori tipici di induttanza vanno dai nanohenry (nH) ai millihenry (mH).
Se un'impedenza di tipo puramente induttivo viene attraversata da una corrente sinusoidale del tipo:
 ,
,
dove IM è il valore di corrente massimo, ω è la pulsazione angolare della sinusoide e φi è la fase della corrente, la tensione che comparirà sul ramo dell'impedenza sarà :
 .
.
Nel ramo di un'impedenza completamente induttiva, quindi, le sinusoidi di tensione e corrente risultano sfasate di 90° e, in particolare, la tensione è in anticipo sulla corrente di 90°.
Nel dominio dei fasori le espressioni di corrente e tensione diventano:
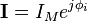
e
 .
.
Dalla legge di Ohm delle impedenze :

si ha che l'impedenza di un induttore puro è:
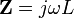 ,
,
dove ω è la pulsazione complessa espressa in radianti al secondo (pari alla frequenza in hertz moltiplicata per 2π), e j è l'unità immaginaria.
Data la relazione costitutiva dell'induttore, la corrente in esso è una funzione continua, mentre la tensione non lo è necessariamente.
In condizioni statiche (DC), l'induttore ideale è equivalente ad un corto circuito.
Data la necessità di inserire un nucleo di ferrite per ottenere valori apprezzabili di induttanza, l'induttore è il componente meno facile da integrare, e quindi viene spesso simulato tramite opportuni componenti attivi (convertitore d'impedenza generalizzato o GIC). A frequenze molto elevate, dell'ordine di parecchi gigahertz, l'impedenza mostrata dall'induttore diventa accettabile anche in presenza di basse induttanze, ed è quindi possibile realizzare induttori senza nucleo (induttore in aria).
Circuito RL [modifica]
Circuito RL in evoluzione libera
Andamento della corrente circolante in L per il circuito RL in evoluzione libera
Si chiama circuito RL in evoluzione libera il circuito mostrato in figura composto da una resistenza e da un induttore percorso da corrente. Evoluzione libera significa che il circuito non ha sorgenti esterne di tensione o di corrente.
Per trattare questo circuito è conveniente usare i teoremi che riguardano le correnti vista la dualità lineare del comportamento dei circuiti tra la tensione e la corrente.
Al tempo t0 = 0 la corrente ai capi di L è  , questa viene presa come condizione iniziale.
, questa viene presa come condizione iniziale.
Applicando la legge di Kirchhoff delle correnti, l'equazione del circuito è:
- (1)

dove i(t) è la corrente elettrica circolante. La relazione caratteristica dell'induttore è ben nota:
- (2)

allora la (1) diventa un'equazione differenziale omogenea del primo ordine:
- (3)

Dalla teoria delle equazioni differenziali la sua soluzione è:
- (4)
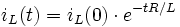
La tensione segue la:
- (5)

Al rapporto ![\frac{L}{R} = \tau \, [s]](http://upload.wikimedia.org/math/3/3/b/33b3e922a580c8231e7fcbce20e1f1a0.png) viene dato il nome di costante di tempo del circuito ed una quantità caratteristica costante del circuito.
viene dato il nome di costante di tempo del circuito ed una quantità caratteristica costante del circuito.
Fisicamente la quantità di corrente contenuta nell'induttore tramite la relazione al momento iniziale, nel momento in cui l'interruttore T viene chiuso, viene scaricata entro il circuito: tale corrente elettrica si dissipa completamente nella resistenza R secondo la legge (4): la corrente tende esponenzialmente a zero per 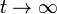 . Il tempo caratteristico di questa caduta di corrente è proprio determinato dalla costante di tempo: essa è il valore dell'istante per il quale la corrente prende il valore di:
. Il tempo caratteristico di questa caduta di corrente è proprio determinato dalla costante di tempo: essa è il valore dell'istante per il quale la corrente prende il valore di:
Circuito RLC [modifica]
![]()
Per approfondire, vedi la voce Circuito RLC.
In generale, si dice RLC un circuito che contenga solo resistenze (R), induttori (L) e condensatori (C). Per estensione, viene spesso definito RLC un circuito che contenga anche altri elementi passivi, ma nessun elemento attivo.
I circuiti RLC sono sistemi lineari, per lo più stazionari (ma non necessariamente). In particolare, ciò significa che un circuito RLC non può creare frequenze dal nulla: può eventualmente sopprimerle. Infatti, la nascita di nuove frequenze (distorsione) avviene soltanto negli elementi attivi a semiconduttore e negli elementi non lineari, come diodi e transistor.
Note [modifica]
Bibliografia [modifica]
- Frederick W. Grover, Inductance Calculations, Dover Publications, New York, 1952.
- Griffiths, David J., Introduction to Electrodynamics (3rd ed.), Prentice Hall, 1998. ISBN 0-13-805326-X
- Roald K. Wangsness, Electromagnetic Fields, 2nd ed., Wiley, 1986. ISBN 0-471-81186-6
- Hughes, Edward., Electrical & Electronic Technology (8th ed.), Prentice Hall, 2002. ISBN 0-582-40519-X
- Küpfmüller K., Einführung in die theoretische Elektrotechnik, Springer-Verlag, 1959.
- Heaviside O., Electrical Papers. Vol.1. – L.; N.Y.: Macmillan, 1892, p. 429-560.
Voci correlate [modifica]
- Autoinduzione
- Forza elettromotrice
- Induzione elettromagnetica
- Mutua induzione
- Circuito RL
- Circuito RLC
歡迎來到Bewise Inc.的世界,首先恭喜您來到這接受新的資訊讓產業更有競爭力,我們是提供專業刀具製造商,應對客戶高品質的刀具需求,我們可以協助客戶滿足您對產業的不同要求,我們有能力達到非常卓越的客戶需求品質,這是現有相關技術無法比擬的,我們成功的滿足了各行各業的要求,包括:精密HSS DIN切削刀具、協助客戶設計刀具流程、DIN or JIS 鎢鋼切削刀具設計、NAS986 NAS965 NAS897 NAS937orNAS907 航太切削刀具,NAS航太刀具設計、超高硬度的切削刀具、醫療配件刀具設計、複合式再研磨機、PCD地板專用企口鑽石組合刀具、粉末造粒成型機、主機版專用頂級電桿、PCD V-Cut刀、捨棄式圓鋸片組、粉末成型機、主機版專用頂級電感、’汽車業刀具設計、電子產業鑽石刀具、木工產業鑽石刀具、銑刀與切斷複合再研磨機、銑刀與鑽頭複合再研磨機、銑刀與螺絲攻複合再研磨機等等。我們的產品涵蓋了從民生刀具到工業級的刀具設計;從微細刀具到大型刀具;從小型生產到大型量產;全自動整合;我們的技術可提供您連續生產的效能,我們整體的服務及卓越的技術,恭迎您親自體驗!!
BW Bewise Inc. Willy Chen willy@tool-tool.com bw@tool-tool.com www.tool-tool.com skype:willy_chen_bw mobile:0937-618-190 Head &Administration Office No.13,Shiang Shang 2nd St., West Chiu Taichung,Taiwan 40356 http://www.tool-tool.com / FAX:+886 4 2471 4839 N.Branch 5F,No.460,Fu Shin North Rd.,Taipei,Taiwan S.Branch No.24,Sec.1,Chia Pu East Rd.,Taipao City,Chiayi Hsien,Taiwan
Welcome to BW tool world! We are an experienced tool maker specialized in cutting tools. We focus on what you need and endeavor to research the best cutter to satisfy users’ demand. Our customers involve wide range of industries, like mold & die, aerospace, electronic, machinery, etc. We are professional expert in cutting field. We would like to solve every problem from you. Please feel free to contact us, its our pleasure to serve for you. BW product including: cutting tool、aerospace tool .HSS DIN Cutting tool、Carbide end mills、Carbide cutting tool、NAS Cutting tool、NAS986 NAS965 NAS897 NAS937orNAS907 Cutting Tools,Carbide end mill、disc milling cutter,Aerospace cutting tool、hss drill’Фрезеры’Carbide drill、High speed steel、Compound Sharpener’Milling cutter、INDUCTORS FOR PCD’CVDD(Chemical Vapor Deposition Diamond )’PCBN (Polycrystalline Cubic Boron Nitride) ’Core drill、Tapered end mills、CVD Diamond Tools Inserts’PCD Edge-Beveling Cutter(Golden Finger’PCD V-Cutter’PCD Wood tools’PCD Cutting tools’PCD Circular Saw Blade’PVDD End Mills’diamond tool. INDUCTORS FOR PCD . POWDER FORMING MACHINE ‘Single Crystal Diamond ‘Metric end mills、Miniature end mills、Специальные режущие инструменты ‘Пустотелое сверло ‘Pilot reamer、Fraises’Fresas con mango’ PCD (Polycrystalline diamond) ‘Frese’POWDER FORMING MACHINE’Electronics cutter、Step drill、Metal cutting saw、Double margin drill、Gun barrel、Angle milling cutter、Carbide burrs、Carbide tipped cutter、Chamfering tool、IC card engraving cutter、Side cutter、Staple Cutter’PCD diamond cutter specialized in grooving floors’V-Cut PCD Circular Diamond Tipped Saw Blade with Indexable Insert’ PCD Diamond Tool’ Saw Blade with Indexable Insert’NAS tool、DIN or JIS tool、Special tool、Metal slitting saws、Shell end mills、Side and face milling cutters、Side chip clearance saws、Long end mills’end mill grinder’drill grinder’sharpener、Stub roughing end mills、Dovetail milling cutters、Carbide slot drills、Carbide torus cutters、Angel carbide end mills、Carbide torus cutters、Carbide ball-nosed slot drills、Mould cutter、Tool manufacturer.
ようこそBewise Inc.の世界へお越し下さいませ、先ず御目出度たいのは新たな
情報を受け取って頂き、もっと各産業に競争力プラス展開。
弊社は専門なエンド・ミルの製造メーカーで、客先に色んな分野のニーズ、
豊富なパリエーションを満足させ、特にハイテク品質要求にサポート致します。
弊社は各領域に供給できる内容は:
(3)鎢鋼エンド・ミル設計
(4)航空エンド・ミル設計
(5)超高硬度エンド・ミル
(7)医療用品エンド・ミル設計
弊社の製品の供給調達機能は:
(4)オートメーション整備調達
弊社の全般供給体制及び技術自慢の総合専門製造メーカーに貴方のご体験を御待ちしております。
Bewise Inc. talaşlı imalat sanayinde en fazla kullanılan ve üç eksende (x,y,z) talaş kaldırabilen freze takımlarından olan Parmak Freze imalatçısıdır. Çok geniş ürün yelpazesine sahip olan firmanın başlıca ürünlerini Karbür Parmak Frezeler, Kalıpçı Frezeleri, Kaba Talaş Frezeleri, Konik Alın Frezeler, Köşe Radyüs Frezeler, İki Ağızlı Kısa ve Uzun Küresel Frezeler, İç Bükey Frezeler vb. şeklinde sıralayabiliriz.
BW специализируется в научных исследованиях и разработках, и снабжаем самым высокотехнологичным карбидовым материалом для поставки режущих / фрезеровочных инструментов для почвы, воздушного пространства и электронной индустрии. В нашу основную продукцию входит твердый карбид / быстрорежущая сталь, а также двигатели, микроэлектрические дрели, IC картонорезальные машины, фрезы для гравирования, режущие пилы, фрезеры-расширители, фрезеры-расширители с резцом, дрели, резаки форм для шлицевого вала / звездочки роликовой цепи, и специальные нано инструменты. Пожалуйста, посетите сайт www.tool-tool.com для получения большей информации.
BW is specialized in R&D and sourcing the most advanced carbide material with high-tech coating to supply cutting / milling tool for mould & die, aero space and electronic industry. Our main products include solid carbide / HSS end mills, micro electronic drill, IC card cutter, engraving cutter, shell end mills, cutting saw, reamer, thread reamer, leading drill, involute gear cutter for spur wheel, rack and worm milling cutter, thread milling cutter, form cutters for spline shaft/roller chain sprocket, and special tool, with nano grade. Please visit our web www.tool-tool.com for more info.

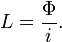




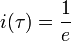
No comments:
Post a Comment