Bewise Inc. www.tool-tool.com Reference source from the internet.
Linear analog electronic filters
Network synthesis filters[hide]
- Butterworth filter
- Chebyshev filter
- Elliptic (Cauer) filter
- Bessel filter
- Gaussian filter
- Optimum "L" (Legendre) filter
- Linkwitz-Riley filter
- Constant k filter
- m-derived filter
- General image filters
- Zobel network (constant R) filter
- Lattice filter (all-pass)
- Bridged T delay equaliser (all-pass)
- Composite image filter
- mm'-type filter
Simple filters[show]
The Butterworth filter is one type of electronic filter design. It is designed to have a frequency response which is as flat as mathematically possible in the passband. Another name for them is 'maximally flat magnitude' filters.
The Butterworth type filter was first described by the British engineer Stephen Butterworth in his paper "On the Theory of Filter Amplifiers", Wireless Engineer (also called Experimental Wireless and the Wireless Engineer), vol. 7, 1930, pp. 536-541.
The Bode plot of a first-order Butterworth low-pass filter
[edit] Overview
The frequency response of the Butterworth filter is maximally flat (has no ripples) in the passband, and rolls off towards zero in the stopband. When viewed on a logarithmic Bode plot, the response slopes off linearly towards negative infinity. For a first-order filter, the response rolls off at −6 dB per octave (−20 dB per decade) (all first-order filters, regardless of name, have the same normalized frequency response). For a second-order Butterworth filter, the response decreases at −12 dB per octave, a third-order at −18 dB, and so on. Butterworth filters have a monotonically changing magnitude function with ω. The Butterworth is the only filter that maintains this same shape for higher orders (but with a steeper decline in the stopband) whereas other varieties of filters (Bessel, Chebyshev, elliptic) have different shapes at higher orders.
Compared with a Chebyshev Type I/Type II filter or an elliptic filter, the Butterworth filter has a slower roll-off, and thus will require a higher order to implement a particular stopband specification. However, Butterworth filter will have a more linear phase response in the passband than the Chebyshev Type I/Type II and elliptic filters.
[edit] A simple example
A third order low pass filter (Cauer topology). The filter becomes a Butterworth filter with cutoff frequency ωc=1 when (for example) C2=4/3 farad, R4=1 ohm, L1=3/2 henry and L3=1/2 henry.
Log density plot of the transfer function H(s) in complex frequency space for the third order Butterworth filter with ωc=1. Note the three poles which lie on a circle of unit radius in the left half plane.
A simple example of a Butterworth filter is the 3rd order low-pass design shown in the figure on the right, with C2 = 4 / 3 farad, R4 = 1 ohm, L1 = 3 / 2 and L3 = 1 / 2 henry. Taking the impedance of the capacitors C to be 1/Cs and the impedance of the inductors L to be Ls, where s = σ + jω is the complex frequency, the circuit equations yields the transfer function for this device:
The magnitude of the frequency response (gain) G(ω) is given by:

and the phase is given by:
Gain and group delay of the third order Butterworth filter with ωc=1
The group delay is defined as the derivative of the phase with respect to angular frequency and is a measure of the distortion in the signal introduced by phase differences for different frequencies. The gain and the delay for this filter are plotted in the graph on the left. It can be seen that there are no ripples in the gain curve in either the passband or the stop band.
The log of the absolute value of the transfer function H(s) is plotted in complex frequency space in the second graph on the right. The function is defined by the three poles in the left half of the complex frequency plane. These are arranged on a circle of radius unity, symmetrical about the real s axis. The gain function will have three more poles on the right half plane to complete the circle.
By replacing each inductor with a capacitor and each capacitor with an inductor, a high-pass Butterworth filter is obtained. If we change each capacitor and inductor into a resonant capacitor and inductor in parallel, with the proper choice of component values, a band-pass Butterworth filter is obtained.
[edit] The transfer function
Plot of the gain of Butterworth low-pass filters of orders 1 through 5. Note that the slope is 20n dB/decade where n is the filter order.
Like all filters, the typical prototype is the low-pass filter, which can be modified into a high-pass filter, or placed in series with others to form band-pass and band-stop filters, and higher order versions of these.
The gain G(ω) of an n-order Butterworth low pass filter is given in terms of the transfer function H(s) as:
where
- n = order of filter
- ωc = cutoff frequency (approximately the -3dB frequency)
- G0 is the DC gain (gain at zero frequency)
It can be seen that as n approaches infinity, the gain becomes a rectangle function and frequencies below ωc will be passed with gain G0, while frequencies above ωc will be suppressed. For smaller values of n, the cutoff will be less sharp.
We wish to determine the transfer function H(s) where s = σ + jω. Since H(s)H(-s) evaluated at s = jω is simply equal to |H(jω)|2, it follows that:
The poles of this expression occur on a circle of radius ωc at equally spaced points. The transfer function itself will be specified by just the poles in the negative real half-plane of s. The k-th pole is specified by:
and hence,
The transfer function may be written in terms of these poles as:
The denominator is a Butterworth polynomial in s.
[edit] Normalized Butterworth polynomials
The Butterworth polynomials may be written in complex form as above, but are usually written with real coefficients by multiplying pole pairs which are complex conjugates, such as s1 and sn. The polynomials are normalized by setting ωc = 1. The normalized Butterworth polynomials then have the general form:
![B_n(s)=\prod_{k=1}^{\frac{n}{2}} \left[s^2-2s\cos\left(\frac{2k+n-1}{2n}\,\pi\right)+1\right]](http://upload.wikimedia.org/math/a/d/4/ad4f4716d76b3e3139307406c199029a.png) for n even
for n even ![B_n(s)=(s+1)\prod_{k=1}^{\frac{n-1}{2}} \left[s^2-2s\cos\left(\frac{2k+n-1}{2n}\,\pi\right)+1\right]](http://upload.wikimedia.org/math/0/1/0/0102df341d364d5ed26a0addf6d6ba66.png) for n odd
for n odd
To four decimal places, they are:
n
Factors of Polynomial Bn(s)
1
(s + 1)
2
s2 + 1.4142s + 1
3
(s + 1)(s2 + s + 1)
4
(s2 + 0.7654s + 1)(s2 + 1.8478s + 1)
5
(s + 1)(s2 + 0.6180s + 1)(s2 + 1.6180s + 1)
6
(s2 + 0.5176s + 1)(s2 + 1.4142s + 1)(s2 + 1.9319s + 1)
7
(s + 1)(s2 + 0.4450s + 1)(s2 + 1.2470s + 1)(s2 + 1.8019s + 1)
8
(s2 + 0.3902s + 1)(s2 + 1.1111s + 1)(s2 + 1.6629s + 1)(s2 + 1.9616s + 1)
[edit] Maximal flatness
Assuming ωc = 1 and G0 = 1, the derivative of the gain with respect to frequency can be shown to be:
which is monotonically decreasing for all ω since the gain G is always positive. The gain function of the Butterworth filter therefore has no ripple. Furthermore, the series expansion of the gain is given by:
In other words, all derivatives of the gain up to but not including the 2n-th derivative are zero, resulting in "maximal flatness".
[edit] High-frequency roll-off
Again assuming ωc = 1, the slope of the log of the gain for large ω is:
In decibels, the high-frequency roll-off is therefore 20n dB/decade, or 6n dB/octave (The factor of 20 is used because the power is proportional to the square of the voltage gain.)
[edit] Filter design
There are a number of different filter topologies available to implement a linear analogue filter. These circuits differ only in the values of the components, but not in their connections.
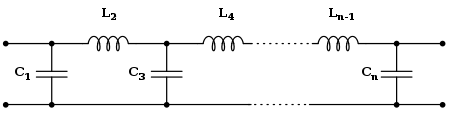
[edit] Cauer topology
The Cauer topology uses passive components (shunt capacitors and series inductors) to implement a linear analog filter. The Butterworth filter having a given transfer function can be realised using a Cauer 1-form. The kth element is given by:
![C_k = 2 \sin \left [\frac {(2k-1)}{2n} \pi \right ]](http://upload.wikimedia.org/math/e/9/1/e912e090b0e30cc8a393c8ea579be580.png) ; k = odd
; k = odd
![L_k = 2 \sin \left [\frac {(2k-1)}{2n} \pi \right ]](http://upload.wikimedia.org/math/4/7/d/47d0b973afc55a9ca878725d302444ff.png) ; k = even
; k = even
The filter may start with a series inductor if desired, in which case the Lk are k odd and the Ck are k even.
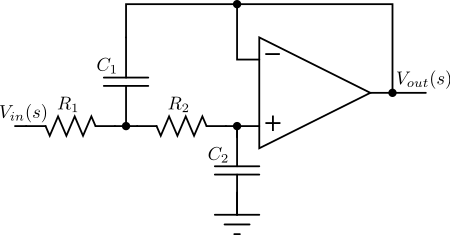
[edit] Sallen-Key topology
The Sallen-Key topology uses active and passive components (op amps and capacitors) to implement a linear analog filter. Each Sallen-Key stage implements a conjugate pair of poles; the overall filter is implemented by cascading all stages in series. If there is a real pole (in the case where n is odd), this must be implemented separately, usually as an RC circuit, and cascaded with the op-amp stages.
The Sallen-Key transfer function is given by
We wish the denominator to be one of the quadratic terms in a Butterworth polynomial. Assuming that ωc = 1, this will mean that
and
This leaves two component values undefined, which may be chosen at will.
[edit] Digital implementation
Digital implementations of Butterworth filters often use bilinear transform or matched z-transform to discretize an analog filter. For higher orders, they are sensitive to quantization errors. For this reason, they are often calculated as cascaded biquad sections and a cascaded first order filter, for odd orders.
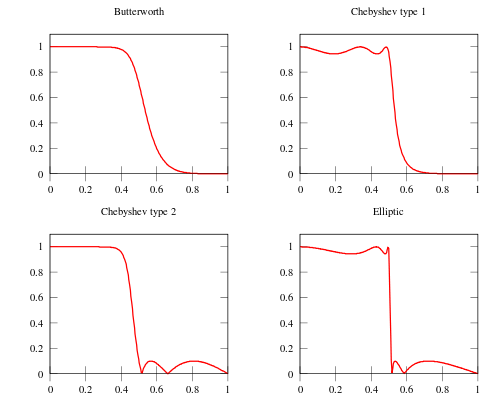
[edit] Comparison with other linear filters
Here is an image showing the gain of a discrete-time Butterworth filter next to other common filter types. All of these filters are fifth-order.
The Butterworth filter rolls off more slowly around the cutoff frequency than the others, but shows no ripples.
歡迎來到Bewise Inc.的世界,首先恭喜您來到這接受新的資訊讓產業更有競爭力,我們是提供專業刀具製造商,應對客戶高品質的刀具需求,我們可以協助客戶滿足您對產業的不同要求,我們有能力達到非常卓越的客戶需求品質,這是現有相關技術無法比擬的,我們成功的滿足了各行各業的要求,包括:精密HSS DIN切削刀具、協助客戶設計刀具流程、DIN or JIS 鎢鋼切削刀具設計、NAS986 NAS965 NAS897 NAS937orNAS907 航太切削刀具,NAS航太刀具設計、超高硬度的切削刀具、醫療配件刀具設計、複合式再研磨機、PCD地板專用企口鑽石組合刀具、NSK高數主軸與馬達、專業模具修補工具-氣動與電動、粉末造粒成型機、主機版專用頂級電桿、PCD V-Cut刀、捨棄式圓鋸片組、粉末成型機、主機版專用頂級電感、’汽車業刀具設計、電子產業鑽石刀具、木工產業鑽石刀具、銑刀與切斷複合再研磨機、銑刀與鑽頭複合再研磨機、銑刀與螺絲攻複合再研磨機等等。我們的產品涵蓋了從民生刀具到工業級的刀具設計;從微細刀具到大型刀具;從小型生產到大型量產;全自動整合;我們的技術可提供您連續生產的效能,我們整體的服務及卓越的技術,恭迎您親自體驗!!
BW Bewise Inc. Willy Chen willy@tool-tool.com bw@tool-tool.com www.tool-tool.com skype:willy_chen_bw mobile:0937-618-190 Head &Administration Office No.13,Shiang Shang 2nd St., West Chiu Taichung,Taiwan 40356 http://www.tool-tool.com / FAX:+886 4 2471 4839 N.Branch 5F,No.460,Fu Shin North Rd.,Taipei,Taiwan S.Branch No.24,Sec.1,Chia Pu East Rd.,Taipao City,Chiayi Hsien,Taiwan
Welcome to BW tool world! We are an experienced tool maker specialized in cutting tools. We focus on what you need and endeavor to research the best cutter to satisfy users’ demand. Our customers involve wide range of industries, like mold & die, aerospace, electronic, machinery, etc. We are professional expert in cutting field. We would like to solve every problem from you. Please feel free to contact us, its our pleasure to serve for you. BW product including: cutting tool、aerospace tool .HSS DIN Cutting tool、Carbide end mills、Carbide cutting tool、NAS Cutting tool、NAS986 NAS965 NAS897 NAS937orNAS907 Cutting Tools,Carbide end mill、disc milling cutter,Aerospace cutting tool、hss drill’Фрезеры’Carbide drill、High speed steel、Compound Sharpener’Milling cutter、INDUCTORS FOR PCD’CVDD(Chemical Vapor Deposition Diamond )’PCBN (Polycrystalline Cubic Boron Nitride) ’Core drill、Tapered end mills、CVD Diamond Tools Inserts’PCD Edge-Beveling Cutter(Golden Finger’PCD V-Cutter’PCD Wood tools’PCD Cutting tools’PCD Circular Saw Blade’PVDD End Mills’diamond tool. INDUCTORS FOR PCD . POWDER FORMING MACHINE ‘Single Crystal Diamond ‘Metric end mills、Miniature end mills、Специальные режущие инструменты ‘Пустотелое сверло ‘Pilot reamer、Fraises’Fresas con mango’ PCD (Polycrystalline diamond) ‘Frese’POWDER FORMING MACHINE’Electronics cutter、Step drill、Metal cutting saw、Double margin drill、Gun barrel、Angle milling cutter、Carbide burrs、Carbide tipped cutter、Chamfering tool、IC card engraving cutter、Side cutter、Staple Cutter’PCD diamond cutter specialized in grooving floors’V-Cut PCD Circular Diamond Tipped Saw Blade with Indexable Insert’ PCD Diamond Tool’ Saw Blade with Indexable Insert’NAS tool、DIN or JIS tool、Special tool、Metal slitting saws、Shell end mills、Side and face milling cutters、Side chip clearance saws、Long end mills’end mill grinder’drill grinder’sharpener、Stub roughing end mills、Dovetail milling cutters、Carbide slot drills、Carbide torus cutters、Angel carbide end mills、Carbide torus cutters、Carbide ball-nosed slot drills、Mould cutter、Tool manufacturer.
ようこそBewise Inc.の世界へお越し下さいませ、先ず御目出度たいのは新たな
情報を受け取って頂き、もっと各産業に競争力プラス展開。
弊社は専門なエンド・ミルの製造メーカーで、客先に色んな分野のニーズ、
豊富なパリエーションを満足させ、特にハイテク品質要求にサポート致します。
弊社は各領域に供給できる内容は:
(3)鎢鋼エンド・ミル設計
(4)航空エンド・ミル設計
(5)超高硬度エンド・ミル
(7)医療用品エンド・ミル設計
弊社の製品の供給調達機能は:
(4)オートメーション整備調達
弊社の全般供給体制及び技術自慢の総合専門製造メーカーに貴方のご体験を御待ちしております。
Bewise Inc. talaşlı imalat sanayinde en fazla kullanılan ve üç eksende (x,y,z) talaş kaldırabilen freze takımlarından olan Parmak Freze imalatçısıdır. Çok geniş ürün yelpazesine sahip olan firmanın başlıca ürünlerini Karbür Parmak Frezeler, Kalıpçı Frezeleri, Kaba Talaş Frezeleri, Konik Alın Frezeler, Köşe Radyüs Frezeler, İki Ağızlı Kısa ve Uzun Küresel Frezeler, İç Bükey Frezeler vb. şeklinde sıralayabiliriz.
BW специализируется в научных исследованиях и разработках, и снабжаем самым высокотехнологичным карбидовым материалом для поставки режущих / фрезеровочных инструментов для почвы, воздушного пространства и электронной индустрии. В нашу основную продукцию входит твердый карбид / быстрорежущая сталь, а также двигатели, микроэлектрические дрели, IC картонорезальные машины, фрезы для гравирования, режущие пилы, фрезеры-расширители, фрезеры-расширители с резцом, дрели, резаки форм для шлицевого вала / звездочки роликовой цепи, и специальные нано инструменты. Пожалуйста, посетите сайт www.tool-tool.com для получения большей информации.
BW is specialized in R&D and sourcing the most advanced carbide material with high-tech coating to supply cutting / milling tool for mould & die, aero space and electronic industry. Our main products include solid carbide / HSS end mills, micro electronic drill, IC card cutter, engraving cutter, shell end mills, cutting saw, reamer, thread reamer, leading drill, involute gear cutter for spur wheel, rack and worm milling cutter, thread milling cutter, form cutters for spline shaft/roller chain sprocket, and special tool, with nano grade. Please visit our web www.tool-tool.com for more info.





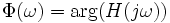






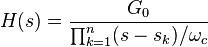






No comments:
Post a Comment