Bewise Inc. www.tool-tool.com Reference source from the internet.
Linear analog electronic filters
Network synthesis filters[hide]
- Butterworth filter
- Chebyshev filter
- Elliptic (Cauer) filter
- Bessel filter
- Gaussian filter
- Optimum "L" (Legendre) filter
- Linkwitz-Riley filter
- Constant k filter
- m-derived filter
- General image filters
- Zobel network (constant R) filter
- Lattice filter (all-pass)
- Bridged T delay equaliser (all-pass)
- Composite image filter
- mm'-type filter
Simple filters[show]
An elliptic filter (also known as a Cauer filter, named after Wilhelm Cauer) is an electronic filter with equalized ripple (equiripple) behavior in both the passband and the stopband. The amount of ripple in each band is independently adjustable, and no other filter of equal order can have a faster transition in gain between the passband and the stopband, for the given values of ripple (whether the ripple is equalized or not). Alternatively, one may give up the ability to independently adjust the passband and stopband ripple, and instead design a filter which is maximally insensitive to component variations.
As the ripple in the stopband approaches zero, the filter becomes a type I Chebyshev filter. As the ripple in the passband approaches zero, the filter becomes a type II Chebyshev filter and finally, as both ripple values approach zero, the filter becomes a Butterworth filter.
The gain of a lowpass elliptic filter as a function of angular frequency ω is given by:
where Rn is the nth-order elliptic rational function (sometimes known as a Chebyshev rational function) and
- ω0 is the cutoff frequency :ε is the ripple factor :ξ is the selectivity factor
The value of the ripple factor specifies the passband ripple, while the combination of the ripple factor and the selectivity factor specify the stopband ripple.
[edit] Properties
The frequency response of a fourth-order elliptic low-pass filter with ε=0.5 and ξ=1.05. Also shown are the minimum gain in the passband and the maximum gain in the stopband, and the transition region between normalized frequency 1 and ξ
A closeup of the transition region of the above plot.
- In the passband, the elliptic rational function varies between zero and unity. The passband of the gain therefore will vary between 1 and
 .
.
- In the stopband, the elliptic rational function varies between infinity and the discrimination factor Ln which is defined as:
- The gain of the stopband therefore will vary between 0 and
 .
.
- In the limit of
 the elliptic rational function becomes a Chebyshev polynomial, and therefore the filter becomes a Chebyshev type I filter, with ripple factor ε
the elliptic rational function becomes a Chebyshev polynomial, and therefore the filter becomes a Chebyshev type I filter, with ripple factor ε
- Since the Butterworth filter is a limiting form of the Chebyshev filter, it follows that in the limit of
 ,
, 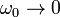 and
and 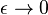 such that
such that  the filter becomes a Butterworth filter
the filter becomes a Butterworth filter
- In the limit of
 ,
, 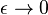 and
and 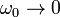 such that ξω0 = 1 and εLn = α, the filter becomes a Chebyshev type II filter with gain
such that ξω0 = 1 and εLn = α, the filter becomes a Chebyshev type II filter with gain
[edit] Poles and zeroes
Log of the absolute value of the gain of an 8th order elliptic filter in complex frequency space (s=σ+jω) with ε=0.5, ξ=1.05 and ω0 = 1. The white spots are poles and the black spots are zeroes. There are a total of 16 poles and 8 double zeroes. What appears to be a single pole and zero near the transition region is actually four poles and two double zeroes as shown in the expanded view below. In this image, black corresponds to a gain of 0.0001 or less and white corresponds to a gain of 10 or more.
An expanded view in the transition region of the above image, resolving the four poles and two double zeroes.
The zeroes of the gain of an elliptic filter will coincide with the poles of the elliptic rational function, which are derived in the article on elliptic rational functions.
The poles of the gain of an elliptic filter may be derived in a manner very similar to the derivation of the poles of the gain of a type I Chebyshev filter. For simplicity, assume that the cutoff frequency is equal to unity. The poles (ωpm) of the gain of the elliptical filter will be the zeroes of the denominator of the gain. Using the complex frequency s = σ + jω this means that:
Defining − js = cd(w,1 / ξ) where cd() is the Jacobi elliptic cosine function and using the definition of the elliptic rational functions yields:
where K = K(1 / ξ) and Kn = K(1 / Ln). Solving for w
where the multiple values of the inverse cd() function are made explicit using the integer index m.
The poles of the elliptic gain function are then:
As is the case for the Chebyshev polynomials, this may be expressed in explicitly complex form (Lutovac 2001 § 12.8)
where ζn is a function of  and ξ and xm are the zeroes of the elliptic rational function. ζn is expressible for all n in terms of Jacobi elliptic functions, or algebraically for some orders, especially orders 1,2, and 3. For orders 1 and 2 we have
and ξ and xm are the zeroes of the elliptic rational function. ζn is expressible for all n in terms of Jacobi elliptic functions, or algebraically for some orders, especially orders 1,2, and 3. For orders 1 and 2 we have
where
The algebraic expression for ζ3 is rather involved (See (Lutovac 2001 § 12.8.1)).
The nesting property of the elliptic rational functions can be used to build up higher order expressions for ζn:
where Lm = Rm(ξ,ξ).
[edit] Minimum Q-factor elliptic filters
The normalized Q-factors of the poles of an 8-th order elliptic filter with ξ=1.1 as a function of ripple factor ε. Each curve represents four poles, since complex conjugate pole pairs and positive-negative pole pairs have the same Q-factor. (The blue and cyan curves nearly coincide). The Q-factor of all poles are simultaneously minimized at εQmin=1/√Ln=0.02323...
See (Lutovac 2001 § 12.11) and (Lutovac 2001 § 13.14)
Elliptic filters are generally specified by requiring a particular value for the passband ripple, stopband ripple and the sharpness of the cutoff. This will generally specify a minimum value of the filter order which must be used. Another design consideration is the sensitivity of the gain function to the values of the electronic components used to build the filter. This sensitivity is inversely proportional to the quality factor (Q-factor) of the poles of the transfer function of the filter. The Q-factor of a pole is defined as:
and is a measure of the influence of the pole on the gain function. For an elliptic filter, it happens that, for a given order, there exists a relationship between the ripple factor and selectivity factor which simultaneously minimizes the Q-factor of all poles in the transfer function:
This results in a filter which is maximally insensitive to component variations, but the ability to independently specify the passband and stopband ripples will be lost. For such filters, as the order increases, the ripple in both bands will decrease and the rate of cutoff will increase. If one decides to use a minimum-Q elliptic filter in order to achieve a particular minimum ripple in the filter bands along with a particular rate of cutoff, the order needed will generally be greater than the order one would otherwise need without the minimum-Q restriction. An image of the absolute value of the gain will look very much like the image in the previous section, except that the poles are arranged in a circle rather than an ellipse. They will not be evenly spaced and there will be zeroes on the ω axis, unlike the Butterworth filter, whose poles are also arranged in a circle.
[edit] Comparison with other linear filters
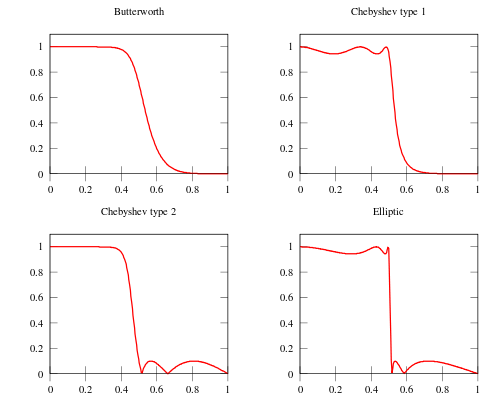
Here is an image showing the elliptic filter next to other common kind of filters obtained with the same number of coefficients:
As is clear from the image, elliptic filters are sharper than all the others, but they show ripples on the whole bandwidth.
[edit] References
- Daniels, Richard W. (1974). Approximation Methods for Electronic Filter Design. New York: McGraw-Hill. ISBN 0-07-015308-6.
- Lutovac, Miroslav D.; Tosic, Dejan V., Evans, Brian L. (2001) (in English). Filter Design for Signal Processing using MATLAB© and Mathematica©. New Jersey, USA: Prentice Hall. ISBN 0-201-36130-2.
歡迎來到Bewise Inc.的世界,首先恭喜您來到這接受新的資訊讓產業更有競爭力,我們是提供專業刀具製造商,應對客戶高品質的刀具需求,我們可以協助客戶滿足您對產業的不同要求,我們有能力達到非常卓越的客戶需求品質,這是現有相關技術無法比擬的,我們成功的滿足了各行各業的要求,包括:精密HSS DIN切削刀具、協助客戶設計刀具流程、DIN or JIS 鎢鋼切削刀具設計、NAS986 NAS965 NAS897 NAS937orNAS907 航太切削刀具,NAS航太刀具設計、超高硬度的切削刀具、醫療配件刀具設計、複合式再研磨機、PCD地板專用企口鑽石組合刀具、NSK高數主軸與馬達、專業模具修補工具-氣動與電動、粉末造粒成型機、主機版專用頂級電桿、PCD V-Cut刀、捨棄式圓鋸片組、粉末成型機、主機版專用頂級電感、’汽車業刀具設計、電子產業鑽石刀具、木工產業鑽石刀具、銑刀與切斷複合再研磨機、銑刀與鑽頭複合再研磨機、銑刀與螺絲攻複合再研磨機等等。我們的產品涵蓋了從民生刀具到工業級的刀具設計;從微細刀具到大型刀具;從小型生產到大型量產;全自動整合;我們的技術可提供您連續生產的效能,我們整體的服務及卓越的技術,恭迎您親自體驗!!
BW Bewise Inc. Willy Chen willy@tool-tool.com bw@tool-tool.com www.tool-tool.com skype:willy_chen_bw mobile:0937-618-190 Head &Administration Office No.13,Shiang Shang 2nd St., West Chiu Taichung,Taiwan 40356 http://www.tool-tool.com / FAX:+886 4 2471 4839 N.Branch 5F,No.460,Fu Shin North Rd.,Taipei,Taiwan S.Branch No.24,Sec.1,Chia Pu East Rd.,Taipao City,Chiayi Hsien,Taiwan
Welcome to BW tool world! We are an experienced tool maker specialized in cutting tools. We focus on what you need and endeavor to research the best cutter to satisfy users’ demand. Our customers involve wide range of industries, like mold & die, aerospace, electronic, machinery, etc. We are professional expert in cutting field. We would like to solve every problem from you. Please feel free to contact us, its our pleasure to serve for you. BW product including: cutting tool、aerospace tool .HSS DIN Cutting tool、Carbide end mills、Carbide cutting tool、NAS Cutting tool、NAS986 NAS965 NAS897 NAS937orNAS907 Cutting Tools,Carbide end mill、disc milling cutter,Aerospace cutting tool、hss drill’Фрезеры’Carbide drill、High speed steel、Compound Sharpener’Milling cutter、INDUCTORS FOR PCD’CVDD(Chemical Vapor Deposition Diamond )’PCBN (Polycrystalline Cubic Boron Nitride) ’Core drill、Tapered end mills、CVD Diamond Tools Inserts’PCD Edge-Beveling Cutter(Golden Finger’PCD V-Cutter’PCD Wood tools’PCD Cutting tools’PCD Circular Saw Blade’PVDD End Mills’diamond tool. INDUCTORS FOR PCD . POWDER FORMING MACHINE ‘Single Crystal Diamond ‘Metric end mills、Miniature end mills、Специальные режущие инструменты ‘Пустотелое сверло ‘Pilot reamer、Fraises’Fresas con mango’ PCD (Polycrystalline diamond) ‘Frese’POWDER FORMING MACHINE’Electronics cutter、Step drill、Metal cutting saw、Double margin drill、Gun barrel、Angle milling cutter、Carbide burrs、Carbide tipped cutter、Chamfering tool、IC card engraving cutter、Side cutter、Staple Cutter’PCD diamond cutter specialized in grooving floors’V-Cut PCD Circular Diamond Tipped Saw Blade with Indexable Insert’ PCD Diamond Tool’ Saw Blade with Indexable Insert’NAS tool、DIN or JIS tool、Special tool、Metal slitting saws、Shell end mills、Side and face milling cutters、Side chip clearance saws、Long end mills’end mill grinder’drill grinder’sharpener、Stub roughing end mills、Dovetail milling cutters、Carbide slot drills、Carbide torus cutters、Angel carbide end mills、Carbide torus cutters、Carbide ball-nosed slot drills、Mould cutter、Tool manufacturer.
ようこそBewise Inc.の世界へお越し下さいませ、先ず御目出度たいのは新たな
情報を受け取って頂き、もっと各産業に競争力プラス展開。
弊社は専門なエンド・ミルの製造メーカーで、客先に色んな分野のニーズ、
豊富なパリエーションを満足させ、特にハイテク品質要求にサポート致します。
弊社は各領域に供給できる内容は:
(3)鎢鋼エンド・ミル設計
(4)航空エンド・ミル設計
(5)超高硬度エンド・ミル
(7)医療用品エンド・ミル設計
弊社の製品の供給調達機能は:
(4)オートメーション整備調達
弊社の全般供給体制及び技術自慢の総合専門製造メーカーに貴方のご体験を御待ちしております。
Bewise Inc. talaşlı imalat sanayinde en fazla kullanılan ve üç eksende (x,y,z) talaş kaldırabilen freze takımlarından olan Parmak Freze imalatçısıdır. Çok geniş ürün yelpazesine sahip olan firmanın başlıca ürünlerini Karbür Parmak Frezeler, Kalıpçı Frezeleri, Kaba Talaş Frezeleri, Konik Alın Frezeler, Köşe Radyüs Frezeler, İki Ağızlı Kısa ve Uzun Küresel Frezeler, İç Bükey Frezeler vb. şeklinde sıralayabiliriz.
BW специализируется в научных исследованиях и разработках, и снабжаем самым высокотехнологичным карбидовым материалом для поставки режущих / фрезеровочных инструментов для почвы, воздушного пространства и электронной индустрии. В нашу основную продукцию входит твердый карбид / быстрорежущая сталь, а также двигатели, микроэлектрические дрели, IC картонорезальные машины, фрезы для гравирования, режущие пилы, фрезеры-расширители, фрезеры-расширители с резцом, дрели, резаки форм для шлицевого вала / звездочки роликовой цепи, и специальные нано инструменты. Пожалуйста, посетите сайт www.tool-tool.com для получения большей информации.
BW is specialized in R&D and sourcing the most advanced carbide material with high-tech coating to supply cutting / milling tool for mould & die, aero space and electronic industry. Our main products include solid carbide / HSS end mills, micro electronic drill, IC card cutter, engraving cutter, shell end mills, cutting saw, reamer, thread reamer, leading drill, involute gear cutter for spur wheel, rack and worm milling cutter, thread milling cutter, form cutters for spline shaft/roller chain sprocket, and special tool, with nano grade. Please visit our web www.tool-tool.com for more info.





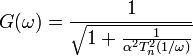



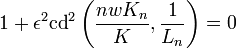

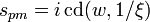





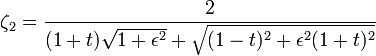





No comments:
Post a Comment