Bewise Inc. www.tool-tool.com Reference source from the internet.
Текущая версия (не проверялась)
Фильтр Баттерворта
Фильтр Баттерво́рта — один из типов электронных фильтров. Фильтры этого класса отличаются от других методом проектирования. Фильтр Баттерворта проектируется так, чтобы его амплитудная частотная характеристика была максимально гладкой на частотах полосы пропускания.
Подобные фильтры были впервые описаны британским инженером Стефаном Баттервортом в статье «О теории фильтрующих усилителей» (англ. On the Theory of Filter Amplifiers), в журнале Wireless Engineer в 1930 году.
[править] Обзор
АЧХ фильтра Баттерворта максимально гладкая на частотах полосы пропускания и снижается практически до нуля на частотах полосы подавления. При отображении частотного отклика фильтра Баттерворта на логарифмической АФЧХ, амплитуда снижается к минус бесконечности на частотах полосы подавления. В случае фильтра первого порядка АЧХ затухает со скоростью −6 децибел на октаву (-20 децибел на декаду) (на самом деле все фильтры первого порядка независимо от типа идентичны и имеют одинаковый частотный отклик). Для фильтра Баттерворта второго порядка АЧХ затухает на −12 дБ на октаву, для фильтра третьего порядка — на −18 дБ и так далее. АЧХ фильтра Баттерворта — монотонно убывающая функция частоты. Фильтр Баттерворта — единственный из фильтров, сохраняющий форму АЧХ для более высоких порядков (за исключением более крутого спада характеристики на полосе подавления) тогда как многие другие разновидности фильтров (фильтр Бесселя, фильтр Чебышева, эллиптический фильтр) имеют различные формы АЧХ при различных порядках.
В сравнении с фильтрами Чебышева I и II типов или эллиптическим фильтром, фильтр Баттерворта имеет более пологий спад характеристики и поэтому должен иметь больший порядок (что более трудно в реализации) для того, чтобы обеспечить нужные характеристики на частотах полосы подавления. Однако фильтр Баттерворта имеет более линейную фазо-частотную характеристику на частотах полосы пропускания.
АЧХ для фильтров Баттерворта нижних частот порядка от 1 до 5. Наклон характерстики — 20n дБ/декаду, где n — порядок фильтра.
Как и для всех фильтров при рассмотрении частотных характеристик используют фильтр нижних частот, из которого легко можно получить фильтр высоких частот, а, включив несколько таких фильтров последовательно, — полосовой фильтр или режекторный фильтр.
Амплитудно-частотная характеристика 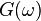 фильтра Баттерворта
фильтра Баттерворта 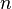 -го порядка может быть получена из передаточной функции
-го порядка может быть получена из передаточной функции 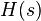 :
:
где
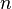 — порядок фильтра
— порядок фильтра  — частота среза (частота на которой амплитуда равна −3dB)
— частота среза (частота на которой амплитуда равна −3dB)  — коэффициент усиления по постоянной составляющей (усиление на нулевой частоте)
— коэффициент усиления по постоянной составляющей (усиление на нулевой частоте)
Легко заметить, что для бесконечных значений 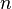 АЧХ становится прямоугольной функцией, и частоты ниже частоты среза будут пропускаться с коэффициентом усиления
АЧХ становится прямоугольной функцией, и частоты ниже частоты среза будут пропускаться с коэффициентом усиления  , а частоты выше частоты среза будут полностью подавляться. Для конечных значений
, а частоты выше частоты среза будут полностью подавляться. Для конечных значений 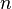 спад характеристики будет пологим.
спад характеристики будет пологим.
С помощью формальной замены 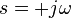 представим выражение
представим выражение  в виде
в виде  :
:
Полюсы передаточной функции расположены на круге радиуса  равноудалённо друг от друга в левой полуплоскости. То есть передаточную функцию фильтра Баттерворта можно определить лишь определением полюсов его передаточной функции в левой полуплоскости s-плоскости.
равноудалённо друг от друга в левой полуплоскости. То есть передаточную функцию фильтра Баттерворта можно определить лишь определением полюсов его передаточной функции в левой полуплоскости s-плоскости. 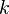 -й полюс определяется из следующего выражения:
-й полюс определяется из следующего выражения:
откуда
Передаточную функцию можно записать в виде:
Аналогичные рассуждения применимы и к цифровым фильтрам Баттерворта, с той лишь разницей, что соотношения записываются не для s-плоскости, а для z-плоскости.
Знаменатель этой передаточной функции называется полиномом Баттерворта.
[править] Нормированные полиномы Баттерворта
Полиномы Баттерворта могут записываться в комплексной форме, как показано выше, однако обычно они записываются в виде соотношений с вещественными коэффициентами (комплексно-сопряжённые пары объединяются с помощью умножения). Нормируются полиномы по частоте среза:  . Нормированные полиномы Баттерворта, таким образом, имеют следующую каноническую форму:
. Нормированные полиномы Баттерворта, таким образом, имеют следующую каноническую форму:
![B_n(s)=\prod_{k=1}^{\frac{n}{2}} \left[s^2-2s\cos\left(\frac{2k+n-1}{2n}\,\pi\right)+1\right]](http://upload.wikimedia.org/math/a/d/4/ad4f4716d76b3e3139307406c199029a.png) ,
, 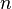 — чётно
— чётно ![B_n(s)=(s+1)\prod_{k=1}^{\frac{n-1}{2}} \left[s^2-2s\cos\left(\frac{2k+n-1}{2n}\,\pi\right)+1\right]](http://upload.wikimedia.org/math/0/1/0/0102df341d364d5ed26a0addf6d6ba66.png) ,
, 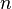 — нечётно
— нечётно
Ниже представлены коэффициенты полиномов Баттерворта для первых восьми порядков:
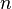
Коэффициенты полиномов 
1
2
3
4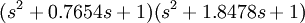
5
6
7
8
[править] Максимальная гладкость
Приняв  и
и  , производная амплитудной характеристики по частоте будет выглядеть следующим образом:
, производная амплитудной характеристики по частоте будет выглядеть следующим образом:
Она монотонно убывает для всех  так как коэффициент усиления всегда положителен. Таким образом, АЧХ фильтра Баттерворта не имеет пульсаций. При разложении амплитудной характеристи в ряд, получим:
так как коэффициент усиления всегда положителен. Таким образом, АЧХ фильтра Баттерворта не имеет пульсаций. При разложении амплитудной характеристи в ряд, получим:
Другими словами, все производные амлитудно-частотной характерситики по частоте до 2n-й равны нулю, из чего следует «максимальная гладкость».
[править] Спад характеристики на высоких частотах
Приняв  , найдём наклон логарифма АЧХ на высоких частотах:
, найдём наклон логарифма АЧХ на высоких частотах:
В децибелах высокочастотная асимптота имеет наклон −20n дБ/декаду.
[править] Проектирование фильтра
Существует ряд различных топологий фильтра, с помощью которых реализуются линейные аналоговые фильтры. Эти схемы отличаются только значениями элементов, структура же остаётся неизменной.
[править] Топология Кауэра
Топология Кауэра использует пассивные элементы (ёмкости и индуктивности). Фильтр Баттеворта с заданной передаточной функцией может быть построен с в форме Кауэра 1 типа. k-й элемент фильтра задаётся соотношением:
![C_k = 2 \sin \left [\frac {(2k-1)}{2n} \pi \right ]](http://upload.wikimedia.org/math/e/9/1/e912e090b0e30cc8a393c8ea579be580.png) ; k чётно
; k чётно
![L_k = 2 \sin \left [\frac {(2k-1)}{2n} \pi \right ]](http://upload.wikimedia.org/math/4/7/d/47d0b973afc55a9ca878725d302444ff.png) ; k нечётно
; k нечётно
[править] Топология Саллена-Кея
Топология Саллена-Кея использует помимо пассивных также и активные элементы (операционные усилители и ёмкости). Каждый каскад схемы Саллена-Кея представляет собой часть фильтра, математически описываемую парой комплексно-сопряжённых полюсов. Весь фильтр получается последовательным соединением всех каскадов. В случае, если попадается действительный полюс, он должен быть реализован отдельно, обычно в виде RC-цепочки, и включён в общую схему.
Передаточная функция каждого каскада в схеме Саллена-Кея имеет вид:
Нужно, чтобы знаменатель представлял собой один из множителей полинома Баттерворта. Приняв  , получим:
, получим:
и
Последнее соотношение даёт две неизвестных, которые могут быть выбраны произвольно.
[править] Сравнение с другими линейными фильтрами
Рисунок ниже показывает АЧХ фильтра Баттерворта в сравнении с другими популярными линейными фильтрами одинакового (пятого) порядка:
Из рисунка видно, что спад АЧХ фильтра Баттерворта самый медленный из четырёх, однако он имеет и самую гладкую АЧХ на частотах полосы пропускания.
[править] Пример
Аналоговый фильтр Баттерворта нижних частот (топология Кауэра) с частотой среза  со следующими номиналами элементов:
со следующими номиналами элементов:  фарад,
фарад,  ом,
ом, 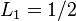 и
и  генри.
генри.
Логарифмический график плотности передаточной функции H(s) на плоскости комплексного аргумента для фильтра Баттерворта третьего порядка с частотой среза  . Три полюса лежат на круге единичного радиуса в левой полуплоскости.
. Три полюса лежат на круге единичного радиуса в левой полуплоскости.
Рассмотрим аналоговый низкочастотный фильтр Баттерворта третьего порядка с  фарад,
фарад,  ом,
ом, 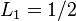 и
и  генри. Обозначив полное сопротивление ёмкостей C как 1/Cs и полное сопротивление индуктивностей L как Ls, где
генри. Обозначив полное сопротивление ёмкостей C как 1/Cs и полное сопротивление индуктивностей L как Ls, где 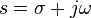 — комплексная переменная, и используя уравнения для расчёта электрических схем, получим следующую передаточную функцию для такого фильтра:
— комплексная переменная, и используя уравнения для расчёта электрических схем, получим следующую передаточную функцию для такого фильтра:
АЧХ 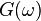 задаётся уравнением:
задаётся уравнением:
а ФЧХ задаётся уравнением:
Групповая задержка определяется как минус производная фазы по круговой частоте и является мерой искажений сигнала по фазе на различных частотах. Логарифмическая АЧХ  такого фильтра не имеет пульсаций ни в полосе пропускания, ни в полосе подавления.
такого фильтра не имеет пульсаций ни в полосе пропускания, ни в полосе подавления.
График модуля передаточной функции на комплексной плоскости ясно указывает на три полюса в левой полуплоскости. Передаточная функция полностью определяется расположением этих полюсов на единичном круге симметрично относительно действительной оси.
Заменив каждую индуктивность ёмкостью, а ёмкости — индуктивностями, получим высокочастотный фильтр Баттерворта.
 и групповая задержка фильтра Баттерворта третьего порядка с частотй среза
и групповая задержка фильтра Баттерворта третьего порядка с частотй среза 
[править] См. также
[править] Библиография
- Лукас В. А. Теория автоматического управления. — М.: Недра, 1990. — 416 с.: ил.
- Справочник по теоретическим основам радиоэлектроники. Ред. Кривицкий Б. Х. Том 2. М.,: Энергия, 1977, с. 305—308.
- Steven W. Smith, The Scientist and Engineer’s Guide to Digital Signal Processing, Second Edition, 1999, California Technical Publishing
- C. Britton Rorabaugh, DSP Primer, McGraw-Hill, 1999.
- Richard J. Higgins, Digital Signal Processing in VLSI, Prentice-Hall, 1990.
- A. V. Oppenheim and R. W. Schafer, Digital Signal Processing, Prentice-Hall, 1975.
- L. R. Rabiner and B. Gold, Theory and Application of Digital Signal Processing, Prentice-Hall, 1975.
- John G. Proakis and Dimitris G. Manolakis, Introduction to Digital Signal Processing, MacMillian, 1988.
- Fredrick J. Harris, On the Use of Windows for Harmonic Analysis with the Discrete Fourier Transform, Proc. IEEE, Vol. 66, No. 1, 1978 pp. 51-83.
- B. Widrow and S.D. Stearns, Adaptive Signal Processing, Prentice-Hall, 1985.
- S. Haykin, Adaptive Filter Theory, 3rd Edition, Prentice-Hall, 1996.
- Michael L. Honig and David G. Messerschmitt, Adaptive Filters — Structures, Algorithms, and Applications, Kluwer Academic Publishers, Hingham, MA 1984.
- J.D. Markel and A.H. Gray, Jr., Linear Prediction of Speech, Springer-Verlag, New York, NY, 1976.
- L.R. Rabiner and R.W. Schafer, Digital Processing of Speech Signals, Prentice-Hall, 1978.
歡迎來到Bewise Inc.的世界,首先恭喜您來到這接受新的資訊讓產業更有競爭力,我們是提供專業刀具製造商,應對客戶高品質的刀具需求,我們可以協助客戶滿足您對產業的不同要求,我們有能力達到非常卓越的客戶需求品質,這是現有相關技術無法比擬的,我們成功的滿足了各行各業的要求,包括:精密HSS DIN切削刀具、協助客戶設計刀具流程、DIN or JIS 鎢鋼切削刀具設計、NAS986 NAS965 NAS897 NAS937orNAS907 航太切削刀具,NAS航太刀具設計、超高硬度的切削刀具、醫療配件刀具設計、複合式再研磨機、PCD地板專用企口鑽石組合刀具、NSK高數主軸與馬達、專業模具修補工具-氣動與電動、粉末造粒成型機、主機版專用頂級電桿、PCD V-Cut刀、捨棄式圓鋸片組、粉末成型機、主機版專用頂級電感、’汽車業刀具設計、電子產業鑽石刀具、木工產業鑽石刀具、銑刀與切斷複合再研磨機、銑刀與鑽頭複合再研磨機、銑刀與螺絲攻複合再研磨機等等。我們的產品涵蓋了從民生刀具到工業級的刀具設計;從微細刀具到大型刀具;從小型生產到大型量產;全自動整合;我們的技術可提供您連續生產的效能,我們整體的服務及卓越的技術,恭迎您親自體驗!!
BW Bewise Inc. Willy Chen willy@tool-tool.com bw@tool-tool.com www.tool-tool.com skype:willy_chen_bw mobile:0937-618-190 Head &Administration Office No.13,Shiang Shang 2nd St., West Chiu Taichung,Taiwan 40356 http://www.tool-tool.com / FAX:+886 4 2471 4839 N.Branch 5F,No.460,Fu Shin North Rd.,Taipei,Taiwan S.Branch No.24,Sec.1,Chia Pu East Rd.,Taipao City,Chiayi Hsien,Taiwan
Welcome to BW tool world! We are an experienced tool maker specialized in cutting tools. We focus on what you need and endeavor to research the best cutter to satisfy users’ demand. Our customers involve wide range of industries, like mold & die, aerospace, electronic, machinery, etc. We are professional expert in cutting field. We would like to solve every problem from you. Please feel free to contact us, its our pleasure to serve for you. BW product including: cutting tool、aerospace tool .HSS DIN Cutting tool、Carbide end mills、Carbide cutting tool、NAS Cutting tool、NAS986 NAS965 NAS897 NAS937orNAS907 Cutting Tools,Carbide end mill、disc milling cutter,Aerospace cutting tool、hss drill’Фрезеры’Carbide drill、High speed steel、Compound Sharpener’Milling cutter、INDUCTORS FOR PCD’CVDD(Chemical Vapor Deposition Diamond )’PCBN (Polycrystalline Cubic Boron Nitride) ’Core drill、Tapered end mills、CVD Diamond Tools Inserts’PCD Edge-Beveling Cutter(Golden Finger’PCD V-Cutter’PCD Wood tools’PCD Cutting tools’PCD Circular Saw Blade’PVDD End Mills’diamond tool. INDUCTORS FOR PCD . POWDER FORMING MACHINE ‘Single Crystal Diamond ‘Metric end mills、Miniature end mills、Специальные режущие инструменты ‘Пустотелое сверло ‘Pilot reamer、Fraises’Fresas con mango’ PCD (Polycrystalline diamond) ‘Frese’POWDER FORMING MACHINE’Electronics cutter、Step drill、Metal cutting saw、Double margin drill、Gun barrel、Angle milling cutter、Carbide burrs、Carbide tipped cutter、Chamfering tool、IC card engraving cutter、Side cutter、Staple Cutter’PCD diamond cutter specialized in grooving floors’V-Cut PCD Circular Diamond Tipped Saw Blade with Indexable Insert’ PCD Diamond Tool’ Saw Blade with Indexable Insert’NAS tool、DIN or JIS tool、Special tool、Metal slitting saws、Shell end mills、Side and face milling cutters、Side chip clearance saws、Long end mills’end mill grinder’drill grinder’sharpener、Stub roughing end mills、Dovetail milling cutters、Carbide slot drills、Carbide torus cutters、Angel carbide end mills、Carbide torus cutters、Carbide ball-nosed slot drills、Mould cutter、Tool manufacturer.
ようこそBewise Inc.の世界へお越し下さいませ、先ず御目出度たいのは新たな
情報を受け取って頂き、もっと各産業に競争力プラス展開。
弊社は専門なエンド・ミルの製造メーカーで、客先に色んな分野のニーズ、
豊富なパリエーションを満足させ、特にハイテク品質要求にサポート致します。
弊社は各領域に供給できる内容は:
(3)鎢鋼エンド・ミル設計
(4)航空エンド・ミル設計
(5)超高硬度エンド・ミル
(7)医療用品エンド・ミル設計
弊社の製品の供給調達機能は:
(4)オートメーション整備調達
弊社の全般供給体制及び技術自慢の総合専門製造メーカーに貴方のご体験を御待ちしております。
Bewise Inc. talaşlı imalat sanayinde en fazla kullanılan ve üç eksende (x,y,z) talaş kaldırabilen freze takımlarından olan Parmak Freze imalatçısıdır. Çok geniş ürün yelpazesine sahip olan firmanın başlıca ürünlerini Karbür Parmak Frezeler, Kalıpçı Frezeleri, Kaba Talaş Frezeleri, Konik Alın Frezeler, Köşe Radyüs Frezeler, İki Ağızlı Kısa ve Uzun Küresel Frezeler, İç Bükey Frezeler vb. şeklinde sıralayabiliriz.
BW специализируется в научных исследованиях и разработках, и снабжаем самым высокотехнологичным карбидовым материалом для поставки режущих / фрезеровочных инструментов для почвы, воздушного пространства и электронной индустрии. В нашу основную продукцию входит твердый карбид / быстрорежущая сталь, а также двигатели, микроэлектрические дрели, IC картонорезальные машины, фрезы для гравирования, режущие пилы, фрезеры-расширители, фрезеры-расширители с резцом, дрели, резаки форм для шлицевого вала / звездочки роликовой цепи, и специальные нано инструменты. Пожалуйста, посетите сайт www.tool-tool.com для получения большей информации.
BW is specialized in R&D and sourcing the most advanced carbide material with high-tech coating to supply cutting / milling tool for mould & die, aero space and electronic industry. Our main products include solid carbide / HSS end mills, micro electronic drill, IC card cutter, engraving cutter, shell end mills, cutting saw, reamer, thread reamer, leading drill, involute gear cutter for spur wheel, rack and worm milling cutter, thread milling cutter, form cutters for spline shaft/roller chain sprocket, and special tool, with nano grade. Please visit our web www.tool-tool.com for more info.






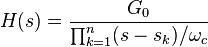





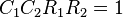





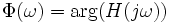

No comments:
Post a Comment