Sunday, March 01, 2009

English Electronic filter www.tool-tool.com

Bewise Inc. www.tool-tool.com Reference source from the internet.

Jump to: navigation, search

Television signal splitter consisting of a high-pass filter (left) and a low-pass filter (right). The antenna is connected to the screw terminals to the left of center.

Electronic filters are electronic circuits which perform signal processing functions, specifically to remove unwanted frequency components from the signal and/or to enhance wanted ones. Electronic filters can be:

The most common types of electronic filters are linear filters, regardless of other aspects of their design. See the article on linear filters for details on their design and analysis.

Contents

[hide]

[edit] History

The oldest forms of electronic filters are passive analog linear filters, constructed using only resistors and capacitors or resistors and inductors. These are known as RC and RL single pole filters respectively. More complex multipole LC filters have also existed for many years and the operation of such filters is well understood with many books having been written about them.

Hybrid filters have also been made, typically involving combinations of analog amplifiers with mechanical resonators or delay lines. Other devices such as CCD delay lines have also been used as discrete-time filters. With the availability of digital signal processing, active digital filters have become common.

[edit] Classification by technology

[edit] Passive filters

Passive implementations of linear filters are based on combinations of resistors (R), inductors (L) and capacitors (C). These types are collectively known as passive filters, because they do not depend upon an external power supply.

Inductors block high-frequency signals and conduct low-frequency signals, while capacitors do the reverse. A filter in which the signal passes through an inductor, or in which a capacitor provides a path to ground, presents less attenuation to low-frequency signals than high-frequency signals and is a low-pass filter. If the signal passes through a capacitor, or has a path to ground through an inductor, then the filter presents less attenuation to high-frequency signals than low-frequency signals and is a high-pass filter. Resistors on their own have no frequency-selective properties, but are added to inductors and capacitors to determine the time-constants of the circuit, and therefore the frequencies to which it responds.

The inductors and capacitors are the reactive elements of the filter. The number of elements determines the order of the filter. In this context, an LC tuned circuit being used in a band-pass or band-stop filter is considered a single element even though it consists of two components.

At high frequencies (above about 100 megahertz), sometimes the inductors consist of single loops or strips of sheet metal, and the capacitors consist of adjacent strips of metal. These inductive or capacitive pieces of metal are called stubs.

[edit] Single element types

A low-pass electronic filter realised by an RC circuit

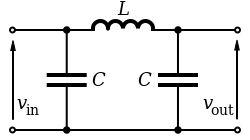
The simplest passive filters consist of a single reactive element. These are constructed of RC, RL, LC or RLC elements.

The quality or "Q" factor is a measure that is sometimes used to describe simple band-pass or band-stop filters. A filter is said to have a high Q if it selects or rejects a range of frequencies that is narrow in comparison to the centre frequency. Q may be defined for bandpass and band-reject filters as the ratio of centre frequency divided by 3dB bandwidth. It is not commonly employed with higher order filters where other parameters are of more concern, and for high-pass or low-pass filters Q is not normally related to bandwidth.

[edit] L filter

An L filter consists of two reactive elements, one in series and one in parallel.

[edit] T and π filters

Low-pass π filter

High-pass T filter

Three-element filters can have a 'T' or 'π' topology and in either geometries, a low-pass, high-pass, band-pass, or band-stop characteristic is possible. The components can be chosen symmetric or not, depending on the required frequency characteristics. The high-pass T filter in the illustration, has a very low impedance at high frequencies, and a very high impedance at low frequencies. That means that it can be inserted in a transmission line, resulting in the high frequencies being passed and low frequencies being reflected. Likewise, for the illustrated low-pass π filter, the circuit can be connected to a transmission line, transmitting low frequencies and reflecting high frequencies. Using m-derived filter sections with correct termination impedances, the input impedance can be reasonably constant in the pass band[1].

[edit] Multiple element types

Multiple element filters are usually constructed as a ladder network. These can be seen as a continuation of the L,T and π designs of filters. More elements are needed when it is desired to improve some parameter of the filter such as stop-band rejection or slope of transition from pass-band to stop-band.

[edit] Active filters

Active filters are implemented using a combination of passive and active (amplifying) components, and require an outside power source. Operational amplifiers are frequently used in active filter designs. These can have high Q, and can achieve resonance without the use of inductors. However, their upper frequency limit is limited by the bandwidth of the amplifiers used.

[edit] Digital filters

A finite impulse response filter

Digital signal processing allows the inexpensive construction of a wide variety of filters. The signal is sampled and an analog to digital converter turns the signal into a stream of numbers. A computer program running on a CPU or a specialized DSP (or less often running on a hardware implementation of the algorithm) calculates an output number stream. This output can be converted to a signal by passing it through a digital to analog converter. There are problems with noise introduced by the conversions, but these can be controlled and limited for many useful filters. Due to the sampling involved, the input signal must be of limited frequency content or aliasing will occur. See also: Digital filter.

[edit] Other filter technologies

[edit] Quartz filters and piezoelectrics

In the late 1930s, engineers realized that small mechanical systems made of rigid materials such as quartz would acoustically resonate at radio frequencies, i.e. from audible frequencies (sound) up to several hundred megahertz. Some early resonators were made of steel, but quartz quickly became favored. The biggest advantage of quartz is that it is piezoelectric. This means that quartz resonators can directly convert their own mechanical motion into electrical signals. Quartz also has a very low coefficient of thermal expansion which means that quartz resonators can produce stable frequencies over a wide temperature range. Quartz crystal filters have much higher quality factors than LCR filters. When higher stabilities are required, the crystals and their driving circuits may be mounted in a "crystal oven" to control the temperature. For very narrow band filters, sometimes several crystals are operated in series.

Engineers realized that a large number of crystals could be collapsed into a single component, by mounting comb-shaped evaporations of metal on a quartz crystal. In this scheme, a "tapped delay line" reinforces the desired frequencies as the sound waves flow across the surface of the quartz crystal. The tapped delay line has become a general scheme of making high-Q filters in many different ways.

[edit] SAW filters

SAW (surface acoustic wave) filters are electromechanical devices commonly used in radio frequency applications. Electrical signals are converted to a mechanical wave in a device constructed of a piezoelectric crystal or ceramic; this wave is delayed as it propagates across the device, before being converted back to an electrical signal by further electrodes. The delayed outputs are recombined to produce a direct analog implementation of a finite impulse response filter. This hybrid filtering technique is also found in an analog sampled filter. SAW filters are limited to frequencies up to 3 GHz.

[edit] BAW filters

BAW (Bulk Acoustic Wave) filters are electromechanical devices. BAW filters can implement ladder or lattice filters. BAW filters typically operate at frequencies from around 2 to around 16 GHz, and in may be smaller or thinner than equivalent SAW filters. Two main variants of BAW filters are making their way into devices, Thin film bulk acoustic resonator or FBAR and Solid Mounted Bulk Acoustic Resonators.

[edit] Garnet filters

Main article: Yttrium iron garnet filter

Another method of filtering, at microwave frequencies from 800 MHz to about 5 GHz, is to use a synthetic single crystal yttrium iron garnet sphere made of a chemical combination of yttrium and iron (YIGF, or yttrium iron garnet filter). The garnet sits on a strip of metal driven by a transistor, and a small loop antenna touches the top of the sphere. An electromagnet changes the frequency that the garnet will pass. The advantage of this method is that the garnet can be tuned over a very wide frequency by varying the strength of the magnetic field.

[edit] Atomic filters

For even higher frequencies and greater precision, the vibrations of atoms must be used. Atomic clocks use caesium masers as ultra-high Q filters to stabilize their primary oscillators. Another method, used at high, fixed frequencies with very weak radio signals, is to use a ruby maser tapped delay line.

[edit] The transfer function

The transfer function \ H(s) of a filter is the ratio of the output signal \ Y(s) to that of the input signal \ X(s) as a function of the complex frequency \ s:

\ H(s)=\frac{Y(s)}{X(s)}

with \ s = \sigma + j \omega.

The transfer function of all linear time-invariant filters generally share certain characteristics:

  • Since the filters are constructed of discrete components, their transfer function will be the ratio of two polynomials in \ s, i.e. a rational function of \ s. The order of the transfer function will be the highest power of \ s encountered in either the numerator or the denominator.
  • The polynomials of the transfer function will all have real coefficients. Therefore, the poles and zeroes of the transfer function will either be real or occur in complex conjugate pairs.
  • Since the filters are assumed to be stable, the real part of all poles (i.e. zeroes of the denominator) will be negative, i.e. they will lie in the left half-plane in complex frequency space.

The proper construction of a transfer function involves the Laplace transform, and therefore it is needed to assume null initial conditions, because

\mathcal{L}\left\{\frac{df}{dt}\right\} = s\cdot\mathcal{L} \left\{ f(t) \right\}-f(0),

And when f(0)=0 we can get rid of the constants and use the usual expression

\mathcal{L}\left\{\frac{df}{dt}\right\} = s\cdot\mathcal{L} \left\{ f(t) \right\}

An alternative to transfer functions is to give the behavior of the filter as a convolution. The convolution theorem, which holds for Laplace transforms, guarantees equivalence with transfer functions.

[edit] Classification by transfer function

Main article: transfer function

Filters may be specified by family and passband. A filter's family is specified by certain design criteria which give general rules for specifying the transfer function of the filter. Some common filter families and their particular design criteria are:

Generally, each family of filters can be specified to a particular order. The higher the order, the more the filter will approach the "ideal" filter. The ideal filter has full transmission in the pass band, and complete attenuation in the stop band, and the transition between the two bands is abrupt (often called brick-wall).

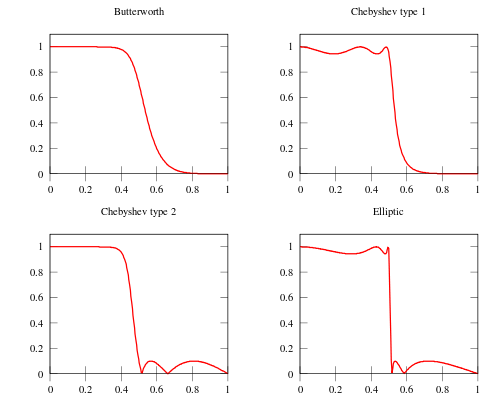
Here is an image comparing Butterworth, Chebyshev, and elliptic filters. The filters in this illustration are all fifth-order low-pass filters. The particular implementation -- analog or digital, passive or active -- makes no difference; their output would be the same.

As is clear from the image, elliptic filters are sharper than all the others, but they show ripples on the whole bandwidth.

Each family can be used to specify a particular pass band in which frequencies are transmitted, while frequencies in the stop band (i.e. outside the pass band) are more or less attenuated.

The family and passband of a filter completely specify the transfer function of a filter. The transfer function completely specifies the behavior of a linear filter, but not the particular technology used to implement it. In other words, there are a number of different ways of achieving a particular transfer function when designing a circuit. A particular pass band filter can be obtained by transformation of a prototype filter of that class.

[edit] Classification by topology

Electronic filters can be classified by the technology used to implement them. Filters using passive filter and active filter technology can be further classified by the particular electronic filter topology used to implement them.

Any given filter transfer function may be implemented in any electronic filter topology.

Some common circuit topologies are:

[edit] Classification by design methodology

Linear analog electronic filters

Network synthesis filters[hide]

Image impedance filters[hide]

Simple filters[hide]

edit

Historically, linear analog filter design has evolved through three major approaches. The oldest designs are simple circuits where the main design criterion was the Q factor of the circuit. This reflected the radio receiver application of filtering as Q was a measure of the frequency selectivity of a tuning circuit. From the 1920s filters began to be designed from the image point of view, mostly being driven by the requirements of telecommunications. After World War II the dominant methodology was network synthesis. The higher mathematics used originally required extensive tables of polynomial coefficient values to be published but modern computer resources have made that unnecessary.[2]

[edit] Direct circuit analysis

Low order filters can be designed by directly applying basic circuit laws such as Kirchoff's laws to obtain the transfer function. This kind of analysis is usually only carried out for simple filters of 1st or 2nd order.

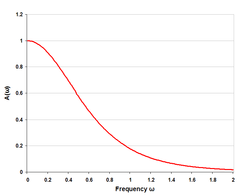
RL filter frequency response

[edit] Image impedance analysis

Main article: Composite image filters

This approach analyses the filter sections from the point of view of the filter being in an infinite chain of identical sections. It has the advantages of simplicity of approach and the ability to easily extend to higher orders. It has the disadvantage that accuracy of predicted responses rely on filter terminations in the image impedance, which is usually not the case.[3]

Constant k filter response with 5 elements

Zobel network (constant R) filter, 5 sections

m-derived filter response, m=0.5, 2 elements

m-derived filter response, m=0.5, 5 elements

[edit] Network synthesis

Main article: Network synthesis filters

The network synthesis approach starts with a required transfer function and then expresses that as a polynomial equation of the input impedance of the filter. The actual element values of the filter are obtained by continued-fraction or partial-fraction expansions of this polynomial. Unlike the image method, there is no need for impedance matching networks at the terminations as the effects of the terminating resistors are included in the analysis from the start.[3]

[edit] See also

[edit] External links and references

  1. ^ The American Radio Relay League, Inc.: "The ARRL Handbook, 1968" page 50
  2. ^ Bray, J, Innovation and the Communications Revolution, Institute of Electrical Engineers
  3. ^ a b Matthaei, Young, Jones Microwave Filters, Impedance-Matching Networks, and Coupling Structures McGraw-Hill 1964

歡迎來到Bewise Inc.的世界，首先恭喜您來到這接受新的資訊讓產業更有競爭力，我們是提供專業刀具製造商，應對客戶高品質的刀具需求，我們可以協助客戶滿足您對產業的不同要求，我們有能力達到非常卓越的客戶需求品質，這是現有相關技術無法比擬的，我們成功的滿足了各行各業的要求，包括：精密HSS DIN切削刀具、協助客戶設計刀具流程、DIN or JIS 鎢鋼切削刀具設計、NAS986 NAS965 NAS897 NAS937orNAS907 航太切削刀具,NAS航太刀具設計、超高硬度的切削刀具、醫療配件刀具設計、複合式再研磨機、PCD地板專用企口鑽石組合刀具、粉末造粒成型機、主機版專用頂級電桿、PCD V-Cut刀、捨棄式圓鋸片組、粉末成型機、主機版專用頂級電感、’汽車業刀具設計、電子產業鑽石刀具、木工產業鑽石刀具、銑刀與切斷複合再研磨機、銑刀與鑽頭複合再研磨機、銑刀與螺絲攻複合再研磨機等等。我們的產品涵蓋了從民生刀具到工業級的刀具設計；從微細刀具到大型刀具；從小型生產到大型量產；全自動整合；我們的技術可提供您連續生產的效能，我們整體的服務及卓越的技術，恭迎您親自體驗！！

BW Bewise Inc. Willy Chen willy@tool-tool.com bw@tool-tool.com www.tool-tool.com skype:willy_chen_bw mobile:0937-618-190 Head &Administration Office No.13,Shiang Shang 2nd St., West Chiu Taichung,Taiwan 40356 http://www.tool-tool.com / FAX:+886 4 2471 4839 N.Branch 5F,No.460,Fu Shin North Rd.,Taipei,Taiwan S.Branch No.24,Sec.1,Chia Pu East Rd.,Taipao City,Chiayi Hsien,Taiwan

Welcome to BW tool world! We are an experienced tool maker specialized in cutting tools. We focus on what you need and endeavor to research the best cutter to satisfy users’ demand. Our customers involve wide range of industries, like mold & die, aerospace, electronic, machinery, etc. We are professional expert in cutting field. We would like to solve every problem from you. Please feel free to contact us, its our pleasure to serve for you. BW product including: cutting tool、aerospace tool .HSS DIN Cutting tool、Carbide end mills、Carbide cutting tool、NAS Cutting tool、NAS986 NAS965 NAS897 NAS937orNAS907 Cutting Tools,Carbide end mill、disc milling cutter,Aerospace cutting tool、hss drill’Фрезеры’Carbide drill、High speed steel、Compound Sharpener’Milling cutter、INDUCTORS FOR PCD’CVDD(Chemical Vapor Deposition Diamond )’PCBN (Polycrystalline Cubic Boron Nitride) ’Core drill、Tapered end mills、CVD Diamond Tools Inserts’PCD Edge-Beveling Cutter(Golden Finger’PCD V-Cutter’PCD Wood tools’PCD Cutting tools’PCD Circular Saw Blade’PVDD End Mills’diamond tool. INDUCTORS FOR PCD . POWDER FORMING MACHINE ‘Single Crystal Diamond ‘Metric end mills、Miniature end mills、Специальные режущие инструменты ‘Пустотелое сверло ‘Pilot reamer、Fraises’Fresas con mango’ PCD (Polycrystalline diamond) ‘Frese’POWDER FORMING MACHINE’Electronics cutter、Step drill、Metal cutting saw、Double margin drill、Gun barrel、Angle milling cutter、Carbide burrs、Carbide tipped cutter、Chamfering tool、IC card engraving cutter、Side cutter、Staple Cutter’PCD diamond cutter specialized in grooving floors’V-Cut PCD Circular Diamond Tipped Saw Blade with Indexable Insert’ PCD Diamond Tool’ Saw Blade with Indexable Insert’NAS tool、DIN or JIS tool、Special tool、Metal slitting saws、Shell end mills、Side and face milling cutters、Side chip clearance saws、Long end mills’end mill grinder’drill grinder’sharpener、Stub roughing end mills、Dovetail milling cutters、Carbide slot drills、Carbide torus cutters、Angel carbide end mills、Carbide torus cutters、Carbide ball-nosed slot drills、Mould cutter、Tool manufacturer.

Bewise Inc. www.tool-tool.com

ようこそＢｅｗｉｓｅ　Ｉｎｃ.の世界へお越し下さいませ、先ず御目出度たいのは新たな

情報を受け取って頂き、もっと各産業に競争力プラス展開。

弊社は専門なエンド・ミルの製造メーカーで、客先に色んな分野のニーズ、

豊富なパリエーションを満足させ、特にハイテク品質要求にサポート致します。

弊社は各領域に供給できる内容は：

（１）精密ＨＳＳエンド・ミルのＲ＆Ｄ

（２）Carbide Cutting tools設計

（３）鎢鋼エンド・ミル設計

（４）航空エンド・ミル設計

（５）超高硬度エンド・ミル

（６）ダイヤモンド・エンド・ミル

（７）医療用品エンド・ミル設計

（８）自動車部品＆材料加工向けエンド・ミル設計

弊社の製品の供給調達機能は：

（１）生活産業～ハイテク工業までのエンド・ミル設計

（２）ミクロ・エンド・ミル～大型エンド・ミル供給

（３）小Ｌｏｔ生産～大量発注対応供給

（４）オートメーション整備調達

（５）スポット対応～流れ生産対応

弊社の全般供給体制及び技術自慢の総合専門製造メーカーに貴方のご体験を御待ちしております。

Bewise Inc. talaşlı imalat sanayinde en fazla kullanılan ve üç eksende (x,y,z) talaş kaldırabilen freze takımlarından olan Parmak Freze imalatçısıdır. Çok geniş ürün yelpazesine sahip olan firmanın başlıca ürünlerini Karbür Parmak Frezeler, Kalıpçı Frezeleri, Kaba Talaş Frezeleri, Konik Alın Frezeler, Köşe Radyüs Frezeler, İki Ağızlı Kısa ve Uzun Küresel Frezeler, İç Bükey Frezeler vb. şeklinde sıralayabiliriz.

BW специализируется в научных исследованиях и разработках, и снабжаем самым высокотехнологичным карбидовым материалом для поставки режущих / фрезеровочных инструментов для почвы, воздушного пространства и электронной индустрии. В нашу основную продукцию входит твердый карбид / быстрорежущая сталь, а также двигатели, микроэлектрические дрели, IC картонорезальные машины, фрезы для гравирования, режущие пилы, фрезеры-расширители, фрезеры-расширители с резцом, дрели, резаки форм для шлицевого вала / звездочки роликовой цепи, и специальные нано инструменты. Пожалуйста, посетите сайт www.tool-tool.com для получения большей информации.

BW is specialized in R&D and sourcing the most advanced carbide material with high-tech coating to supply cutting / milling tool for mould & die, aero space and electronic industry. Our main products include solid carbide / HSS end mills, micro electronic drill, IC card cutter, engraving cutter, shell end mills, cutting saw, reamer, thread reamer, leading drill, involute gear cutter for spur wheel, rack and worm milling cutter, thread milling cutter, form cutters for spline shaft/roller chain sprocket, and special tool, with nano grade. Please visit our web www.tool-tool.com for more info.

Bewise Inc 位於

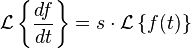
No comments:

Post a Comment

Subscribe to: Post Comments (Atom)